如图，直线a、b被直线c、d所截，若∠1=∠2，∠3=115°，则∠4的度数为（ ）
A．55° B．60° C．65° D．75°
阅读快车系列答案科目：初中数学 来源： 题型：
下列事件中，属于必然事件的是（ ）
A． 购买一张彩票，中奖 Ｂ．打开电视，正在播放广告
Ｃ．抛掷一枚硬币，正面向上 Ｄ．通常情况下，水加热到100℃沸腾
查看答案和解析>>
科目：初中数学 来源： 题型：
抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图所示，则下列结论：
①4ac﹣b2＜0；
②若点（x1，y1）在抛物线上，且x1≠﹣1，则有a﹣ax12＞bx1+b；
③a+b+c＜0；
④点M（x1，y1）、N（x2，y2）在抛物线上，若x1＜x2，则y1≤y2，
其中正确结论的个数是（ ）
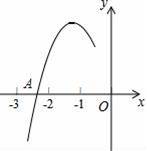
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，已知二次函数y=﹣x2+bx+c的图象经过A（﹣2，﹣1），B（0，7）两点．
（1）求该抛物线的解析式及对称轴；
（2）当x为何值时，y＞0？
（3）在x轴上方作平行于x轴的直线l，与抛物线交于C，D两点（点C在对称轴的左侧），过点C，D作x轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
某市为缓解城市交通压力，决定修建人行天桥，原设计天桥的楼梯长AB=6m，∠ABC=45°，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使∠ADC=30°（如图所示）．
（1）求调整后楼梯AD的长；
（2）求BD的长．
（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系xOy中，已知点A的坐标为（3，a）（其中a＞4），射线OA与反比例函数y=
的图象交于点P，点B、C分别在函数y=的图象上，且AB∥x轴，AC∥y 轴；
（1）当点P横坐标为2，求直线AO的表达式；
（2）连接CO，当AC=CO时，求点A坐标；
（3）连接BP、CP，试猜想：
的值是否随a的变化而变化？如果不变，求出的值；如果变化，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
a，满足
，求
的
tan60°+（﹣
）﹣1+|4|