
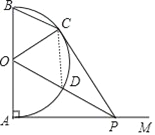
【题目】如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空:
①当AP= 时,四边形OAPC是正方形;
②当AP= 时,四边形BODC是菱形.

【答案】(1)证明见解析;(2)①2;②2![]() .
.
【解析】试题分析:(1)根据切线的性质,可以得到OP⊥AC,然后利用“HL”证明:△OAP≌△OCP;
(2)①根据正方形的性质可以得到AP的长;
②先利用菱形的性质得到△OBC为等边三角形,则∠B=60°,所以∠AOP=60°,然后在Rt△OAP中利用正切的定义求AP即可.
试题解析:(1)∵PC切半圆O于点C,∴OC⊥PC,
∵AM⊥AB,∴∠OAP=90°,
在Rt△OAP和Rt△OCP中![]() ,∴Rt△OAP≌Rt△OCP;
,∴Rt△OAP≌Rt△OCP;
(2)①∵Rt△OAP≌Rt△OCP,∴PA=PC,
而OA=OC,∴当AO=AP时,四边形OAPC为菱形,
而∠OAP=90°,∴四边形OAPC是正方形,此时AP=OA=2;
②∵四边形BODC是菱形,∴OB=OD=CD=BC,BC∥OD,∴△OBC为等边三角形,
∴∠B=60°,∴∠AOP=60°,
在Rt△OAP中,∵tan∠AOP=![]() ,∴AP=2tan60°=2
,∴AP=2tan60°=2![]() ,
,
即AP=2![]() 时,四边形BODC是菱形.
时,四边形BODC是菱形.
故答案为2,2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒

当t = 4时,求线段PQ的长度
(2)当t为何值时,△PCQ是等腰三角形?
(3)当t为何值时,△PCQ的面积等于16cm2?
(4)当t为何值时,△PCQ∽△ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小韦随机调查了若干市民租用共享单车后骑车时间![]() (单位:分),将获得的数据分成四组,绘制了如下统计图.请根据图中信息,解答下列问题:
(单位:分),将获得的数据分成四组,绘制了如下统计图.请根据图中信息,解答下列问题:
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
上课时李老师提出这样一个问题:对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,求a的取值范围.
小捷的思路是:原不等式等价于x2﹣2x﹣1>a,设函数y1=x2﹣2x﹣1,y2=a,画出两个函数的图象的示意图,于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围.
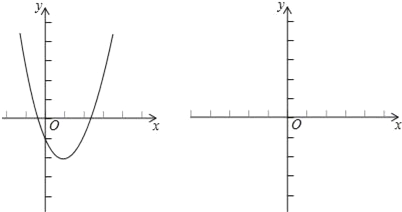
请结合小捷的思路回答:
对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,则a的取值范围是 .
参考小捷思考问题的方法,解决问题:
关于x的方程x﹣4=![]() 在0<a<4范围内有两个解,求a的取值范围.
在0<a<4范围内有两个解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com