
����Ŀ���Ķ�������ϣ�
�Ͽ�ʱ����ʦ�������һ�����⣺��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ��
С�ݵ�˼·�ǣ�ԭ����ʽ�ȼ���x2��2x��1��a���躯��y1=x2��2x��1��y2=a����������������ͼ���ʾ��ͼ������ԭ����ת��Ϊ����y1��ͼ����y2��ͼ���Ϸ�ʱa��ȡֵ��Χ��
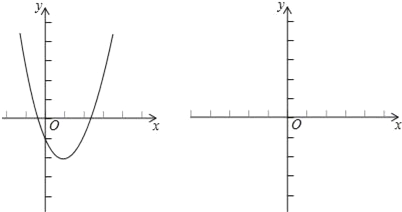
����С�ݵ�˼·�ش�
��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ���� ����
�ο�С��˼������ķ�����������⣺
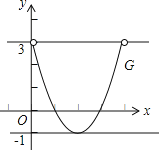
����x�ķ���x��4=![]() ��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
���𰸡���1��a����2����2����1��a��3
���������������������С�ݵ�˼·�ش�ֱ�Ӹ��ݺ����Ķ�������ɵó�a��ȡֵ��Χ����y1=x2-4x+3��y2=a���Ǻ���y1��0��x��4�ڵ�ͼ��ΪG������ԭ����ת��Ϊy2=a��G����������ʱa��ȡֵ��Χ�����ͼ��ɵó�������
���������
�⣺����С�ݵ�˼·�ش�
�ɺ���ͼ���֪��a����2ʱ������x�IJ���ʽx2��2x��1��a��0�������
�ʴ�Ϊ��a����2��
������⣺��ԭ����ת��Ϊx2��4x+3=a��
��y1=x2��4x+3��y2=a���Ǻ���y1��0��x��4�ڵ�ͼ��ΪG������ԭ����ת��Ϊy2=a��G����������ʱa��ȡֵ��Χ�����ͼ���֪��a��ȡֵ��Χ�ǣ���1��a��3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ���Ķ�����������,�ö���,������,������������.Ϊ����ͬѧ�ǵĶ�������,ѧУͼ��������»����ɹ���ѧ�����Ͷ���������ͼ��.���˽�,20����ѧ������40�������鹲��1 520Ԫ,20����ѧ������20���������440Ԫ(ע:���ɹ�����ѧ�����۸�һ��,���ɹ��Ķ�����۸�һ��).
��1��ÿ����ѧ����Ԫ,ÿ��������Ԫ;
��2����ѧУҪ�����������ѧ������20��,���������ѧ�����ܱ���������72��,�ܷ��ò�����2 000Ԫ,��������з��������Ĺ��鷽��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ı���ABCDΪ��O�ڽ��ı��Σ�����AC��CO��BO����CΪ��BD���е㣮
��1����֤����DAC=��ACO+��ABO��
��2����ͼ2����E��OC�ϣ�����EB���ӳ�CO��AB�ڵ�F������DAB=��OBA+��EBA����֤��EF=EB��
��3���ڣ�2���������£���ͼ3����OE+EB=AB��CE=2��AB=13����AD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P����2��4�����ڵ������ǣ�������
A. �������� B. �ڶ����� C. ��һ���� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���������( )
A.����7x+ ![]() =0�Ľ�,����ֱ��y=7x+
=0�Ľ�,����ֱ��y=7x+ ![]() ��x�ύ��ĺ�����
��x�ύ��ĺ�����
B.����2x+3=4x+7�Ľ�,����ֱ��y=2x+3��ֱ��y=4x+7����ĺ�����
C.����7x+ ![]() =0�Ľ�,����һ�κ���y=7x+
=0�Ľ�,����һ�κ���y=7x+ ![]() ������ֵΪ0ʱ�Ա�����ֵ
������ֵΪ0ʱ�Ա�����ֵ
D.����7x+ ![]() =0�Ľ�,����ֱ��y=7x+
=0�Ľ�,����ֱ��y=7x+ ![]() ��y�ύ���������
��y�ύ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ��������AM��AB����P��AM�ϣ�����OP����ԲO�ڵ�D��PC�а�ԲO�ڵ�C������BC��OC��
��1����֤����OAP�ա�OCP��
��2������ԲO�İ뾶����2����գ�
�ٵ�AP= �� ��ʱ���ı���OAPC�������Σ�
�ڵ�AP=�� ��ʱ���ı���BODC�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���ABCD�������Σ�E��CD���е㣬P��BC���ϵ�һ�㣬�����������١�APB����EPC���ڡ�APE����APB����P��BC���е㣻��BP��BC��2��3.�������Ƴ���ABP�ס�ECP����(����)

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������
��1����-10��+��+7���� ��2����-45��+��-39��
��3����-3��-��-7�� ��4��33-��-27��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
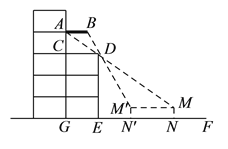
����Ŀ����ĩ��С����ͬѧ����Ƥ�ߣ�ȥ�������ү��¶̨������Ŀ��ȣ���ͼ��������ֱ�Ӳ�����С������¥ǰ������ѡ����һ��ֱ��![]() ��ͨ����ֱ��
��ͨ����ֱ��![]() ��ѡ��۲⣬���ֵ���λ��
��ѡ��۲⣬���ֵ���λ��![]() ��ʱ���������ߴ�
��ʱ���������ߴ�![]() ��ͨ��¶̨
��ͨ��¶̨![]() ����������������
����������������![]() �㴦������λ��
�㴦������λ��![]() ��ʱ�����ߴ�
��ʱ�����ߴ�![]() ��ͨ��
��ͨ��![]() ����������������
����������������![]() �㴦�������۲��������
�㴦�������۲��������![]() ��
��![]() ��ľ��뼴Ϊ������Ŀ�����֪
��ľ��뼴Ϊ������Ŀ�����֪![]() ����
����![]() ��
��![]() �ϣ�
�ϣ� ![]() ��
��![]() ��
��![]() ��
��![]() ����ֱ��
����ֱ��![]() ��
�� ![]() ��¶̨�Ŀ�
��¶̨�Ŀ�![]() �����
�����![]() �ף�
�ף� ![]() �ף�
�ף� ![]() �ף��������������Ϣ�����������Ŀ�
�ף��������������Ϣ�����������Ŀ�![]() �Ƕ����ף��������ȷ��
�Ƕ����ף��������ȷ��![]() �ף���
�ף���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com