练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】基础计算

    （1）（-10）+（+7）； （2）（-45）+（-39）

    （3）（-3）-（-7） （4）33-（-27）

    【答案】（1）-3；（2）-84；（3）4；（4）60．

    【解析】

    （1）根据有理数加法法则进行计算即可；

    （2）根据有理数加法法则进行计算即可；

    （3）根据有理数减法法则进行计算即可；

    （4）根据有理数减法法则进行计算即可．

    解（1）(-10)+(+7)=-(10-7)=-3；

    （2）(-45)+(-39)=-(45+39)=-84；

    （3）(-3)-(-7)=(-3)+7=4；

    （4）33-(-27)=33+27=60．

    故答案为（1）-3；（2）-84；（3）4；（4）60．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是( )
    A.a3·a2=a6
    B.(a2)3=a6
    C.(2a2)3=6a6
    D.(-2a3)2=-4a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    上课时李老师提出这样一个问题：对于任意实数x，关于x的不等式x2﹣2x﹣1﹣a＞0恒成立，求a的取值范围．

    小捷的思路是：原不等式等价于x2﹣2x﹣1＞a，设函数y1=x2﹣2x﹣1，y2=a，画出两个函数的图象的示意图，于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围．

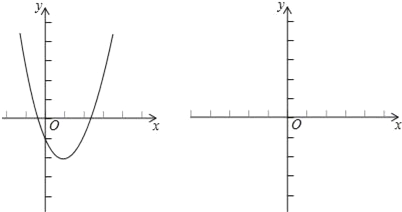
    请结合小捷的思路回答：

    对于任意实数x，关于x的不等式x2﹣2x﹣1﹣a＞0恒成立，则a的取值范围是　 　．

    参考小捷思考问题的方法，解决问题：

    关于x的方程x﹣4=在0＜a＜4范围内有两个解，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果抛物线y=mx2+（m﹣3）x﹣m+2经过原点，那么m= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中，正确的个数有（ ）
    ①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为 ；
    ②直角三角形的最大边长为 ，最短边长为1，则另一边长为 ；
    ③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；
    ④等腰三角形面积为12，底边上的高为4，则腰长为5．
    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果a+3和2a﹣6是一个数的平方根，这个数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A，B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120nmile，乙巡逻艇每小时航行50nmile，航向为北偏西40°，问：甲巡逻艇的航向是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地，两车同时出发．不久，第二列快车也从甲地发往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分后，第二列快车与慢车相遇．设慢车行驶的时间为x（单位：时），慢车与第一、第二列快车之间的距离y（单位：千米）与x（单位：时）之间的函数关系如图1、图2，根据图象信息解答下列问题：

    （1）甲、乙两地之间的距离为_____千米．

    （2）求图1中线段CD所表示的y与x之间的函数关系式，并写出自变量x的取值范围．

    （3）请直接在图2中的（____）内填上正确的数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】等腰三角形其中两条边的长度为5和11,则该等腰三角形的周长为（ ）

    A. 21B. 27C. 21或32D. 21或27

    查看答案和解析>>

    同步练习册答案