[题目]如图.在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲.乙两艘巡逻艇立即从相距13nmile的A.B两个基地前去拦截.六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120nmile.乙巡逻艇每小时航行50nmile.航向为北偏西40°.问:甲巡逻艇的航向是多少? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A，B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120nmile，乙巡逻艇每小时航行50nmile，航向为北偏西40°，问：甲巡逻艇的航向是多少？

【答案】解：AC=120×=12(nmile)，BC=50×=5(nmile)，又因为AB=13nmile，所以AC2+BC2=AB2 ，所以△ABC是直角三角形，可知∠CAB+∠CBA=90°，由∠CBA=50°，知∠CAB=40°，所以甲巡逻艇的航向为北偏东50°
【解析】运用勾股定理的逆定理可判断△ABC是直角三角形，再根据直角三角形两锐角互余可求甲巡逻艇的航向。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图1，四边形ABCD为⊙O内接四边形，连接AC、CO、BO，点C为弧BD的中点．

（1）求证：∠DAC=∠ACO+∠ABO；

（2）如图2，点E在OC上，连接EB，延长CO交AB于点F，若∠DAB=∠OBA+∠EBA．求证：EF=EB；

（3）在（2）的条件下，如图3，若OE+EB=AB，CE=2，AB=13，求AD的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，四边形ABCD是正方形，E是CD的中点，P是BC边上的一点，下列条件：①∠APB＝∠EPC；②∠APE＝∠APB；③P是BC的中点；④BP∶BC＝2∶3.其中能推出△ABP∽△ECP的有(　　)

A. 1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】基础计算

（1）（-10）+（+7）；（2）（-45）+（-39）

（3）（-3）-（-7）（4）33-（-27）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知八边形ABCDEFGH中4个正方形的面积分别为25，144，48，121个平方单位，PR=13（单位），则该八边形的面积= 平方单位．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】三角形纸片内有100个点，连同三角形的顶点共103个点，其中任意三点都不共线．现以这些点为顶点作三角形，并把纸片剪成小三角形，这样的小三角形的个数是（）
A.299
B.201
C.205
D.207

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】随着人民生活水平的提高，购买老年代步车的人越来越多．这些老年代步车却成为交通安全的一大隐患．针对这种现象，某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查，其中调查问卷设置以下选项（只选一项）：

A：加强交通法规学习；

B：实行牌照管理；

C：加大交通违法处罚力度；

D：纳入机动车管理；

E：分时间分路段限行

调查数据的部分统计结果如下表：

管理措施	回答人数	百分比
A	25	5%
B	100	m
C	75	15%
D	n	35%
E	125	25%
合计	a	100%

（1）根据上述统计表中的数据可得m=_____，n=_____，a=_____；

（2）在答题卡中，补全条形统计图；

（3）该社区有居民2600人，根据上述调查结果，请你估计选择“D：纳入机动车管理”的居民约有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：

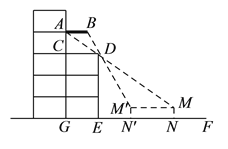
【题目】周末，小凯和同学带着皮尺，去测量杨大爷家露台遮阳蓬的宽度．如图，由于无法直接测量，小凯便在楼前地面上选择了一条直线，通过在直线上选点观测，发现当他位于点时，他的视线从点通过露台点正好落在遮阳蓬点处；当他位于点时，视线从点通过点正好落在遮阳蓬点处，这样观测到的两个点、间的距离即为遮阳蓬的宽．已知，点在上，、、、均垂直于，，露台的宽，测得米，米，米．请你根据以上信息，求出遮阳蓬的宽是多少米？（结果精确到米）．