
【题目】结合数轴与绝对值的知识回答下列问题:
(1)探究:
①数轴上表示5和2的两点之间的距离是___.
②数轴上表示2和6的两点之间的距离是___.
③数轴上表示4和3的两点之间的距离是___.
(2)归纳:
一般的,数轴上表示数m和数n的两点之间的距离等于|mn|.
(3)应用:
①如果表示数a和3的两点之间的距离是7,则可记为:|a3|=7,那么a=___.
![]()
②若数轴上表示数a的点位于4与3之间,求|a+4|+|a3|的值.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
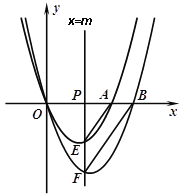
【题目】如图,动直线![]() (
(![]() )分别交x轴,抛物线
)分别交x轴,抛物线![]() 和
和![]() 于点P,E,F,设点A,B为抛物线
于点P,E,F,设点A,B为抛物线![]() ,
, ![]() 与x轴的一个交点,连结AE,BF.
与x轴的一个交点,连结AE,BF.
(1)求点A,B的坐标.
(2)当![]() 时,判断直线AE与BF的位置关系,并说明理由.
时,判断直线AE与BF的位置关系,并说明理由.
(3)连结BE,当![]() 时,求△BEF的面积.
时,求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:

(1)本次调查的学生人数为__________,娱乐节目在扇形统计图中所占圆心角的度数是__________度.
(2)请将条形统计图补充完整:
(3)若该中学有2000名学生,请估计该校喜爱动画节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,tanB=2。



(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF,求证:DF-EF=![]() AF;
AF;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论为____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() ,点
,点![]() 是线段
是线段![]() 延长线一点,连结
延长线一点,连结![]() ,
,![]() ,
,![]()
(1)将线段![]() 沿着射线
沿着射线![]() 运动,使得点
运动,使得点![]() 与点
与点![]() 重合,用代数式表示线段
重合,用代数式表示线段![]() 扫过的平面部分的面积.
扫过的平面部分的面积.
(2)将三角形![]() 绕着点
绕着点![]() 旋转,使得
旋转,使得![]() 与
与![]() 重合,点
重合,点![]() 落在点
落在点![]() ,用代数式表示线段
,用代数式表示线段![]() 扫过的平面部分的面积.
扫过的平面部分的面积.
(3)将三角形![]() 顺时针旋转,使旋转后的三角形有一边与正方形的一边完全重合(第(2)小题的情况除外),请在如图中画出符合条件的3种情况,并写出相应的旋转中心和旋转角
顺时针旋转,使旋转后的三角形有一边与正方形的一边完全重合(第(2)小题的情况除外),请在如图中画出符合条件的3种情况,并写出相应的旋转中心和旋转角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字,根据所给信息解答下面问题:把几个数用大括号括起来,中间用逗号隔开,如:{3,4};{﹣3,6,8,18},其中大括号内的数称其为集合的元素.如果一个集合满足:只要其中有一个元素a,使得﹣2a+4也是这个集合的元素,这样的集合称为条件集合.例如;{3,﹣2},因为﹣2×3+4=﹣2,﹣2恰好是这个集合的元素所以吕{3,﹣2}是条件集合:例如;(﹣2,9,8,},因为﹣2×(﹣2)+4=8,8恰好是这个集合的元素,所以{﹣2,9,8,}是条件集合.
(1)集合{﹣4,12}是否是条件集合?
(2)集合{![]() ,﹣
,﹣![]() ,
,![]() }是否是条件集合?
}是否是条件集合?
(3)若集合{8,n}和{m}都是条件集合.求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮胎的直径是否符合标准,是判断轮胎质量的好与差的重要依据之一.东风轮胎厂某批轮胎的标准直径是600mm,质量检验员从这批产品中抽取10个轮胎进行检查,超过标准直径的毫米数记为正,不足的毫米数记为负,检查记录如下(单位:mm):
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
检查结果 |
|
|
| 0 |
|
|
|
|
|
|
(
(2)求这10个轮胎的平均直径(精确到![]() mm).
mm).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com