
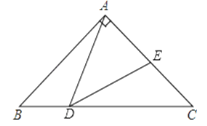
【题目】如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
(1)求证:△ABD∽△DCE;
(2)当△ADE是等腰三角形时,求AE的长.
【答案】(1)见解析;(2)1
【解析】
(1)首先根据等腰直角三角形的两个底角都是45![]() ,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
,得到一对对应角相等;再根据三角形的外角的性质得到∠ADE+∠EDC=∠B+∠BAD,从而证明∠EDC=∠BAD,根据两个角对应相等,得到两个三角形相似;
(2)根据等腰三角形的定义,此题要分AD=AE、AD=DE、AE=DE三种情况进行分析讨论.
(1)证明:Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°.
∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=45°,
∴45°+∠EDC=45°+∠BAD.
∴∠EDC=∠BAD.
∴△ABD∽△DCE.
(2)解:讨论:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意.
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=2,BC=2![]() ,AE=AC﹣EC=2﹣BD=2﹣(2
,AE=AC﹣EC=2﹣BD=2﹣(2![]() ﹣2)=4﹣2
﹣2)=4﹣2![]()
③若AE=DE,此时∠DAE=∠ADE=45°,
如下图所示易知AD⊥BC,DE⊥AC,且AD=DC.由等腰三角形的三线合一可知:AE=CE=![]() AC=1.
AC=1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于点A(﹣2,﹣5),C(5,n),交y轴于点B,交x轴于点D.
的图象交于点A(﹣2,﹣5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数![]() 和一次函数y1=kx+b的表达式;
和一次函数y1=kx+b的表达式;
(2)连接OA,OC,求△AOC的面积;
(3)根据图象,直接写出y1>y2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
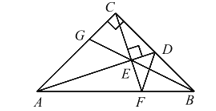
【题目】如图:Rt△ABC 中,AC=BC,∠ACB=90°,D 为 BC 边中点,CF⊥AD 交 AD 于 E,交 AB 于 F,BE交 AC 于 G,连 DF,下列结论:①AC=AF,②CD+DF=AD,③∠ADC=∠BDF,④CE=BE,⑤∠ BED=45°,其中正确的有( )
A. 5 个B. 4 个C. 3 个D. 2 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
我区在一项工程招标时,接到甲、乙两个工程队的投标书,从投标书中得知:每施工一天,甲工程队要![]() 万元,乙工程队要
万元,乙工程队要![]() 万元,工程小组根据甲、乙两队标书的测算,有三种方案:
万元,工程小组根据甲、乙两队标书的测算,有三种方案:![]() 甲队单独完成这个工程,刚好如期完成;
甲队单独完成这个工程,刚好如期完成;![]() 乙队单独完成这个工程要比规定时间多用5天;
乙队单独完成这个工程要比规定时间多用5天;![]() **********,剩下的工程由乙队单独做,也正好如期完成. 方案
**********,剩下的工程由乙队单独做,也正好如期完成. 方案![]() 中“星号”部分被损毁了. 已知,一个同学设规定的工期为
中“星号”部分被损毁了. 已知,一个同学设规定的工期为![]() 天,根据题意列出方程:
天,根据题意列出方程:![]()
(1)请将方案中“星号”部分补充出来________________;
(2)你认为哪个方案节省工程款,请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
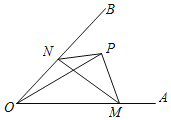
【题目】如图,∠AOB=45°,点P是∠AOB内的定点且OP=![]() ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是_____.
,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如,图中过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线.与坐标轴围成矩形
轴的垂线.与坐标轴围成矩形![]() 的周长的数值与面积的数值相等,则点
的周长的数值与面积的数值相等,则点![]() 是和谐点.
是和谐点.

(1)判断点![]() ,
,![]() 是否为和谐点,并说明理由;
是否为和谐点,并说明理由;
(2)若和谐点![]() 在直线
在直线![]() (
(![]() 为常数)上,求
为常数)上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为等边三角形,
为等边三角形,![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合)以
重合)以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() .
.
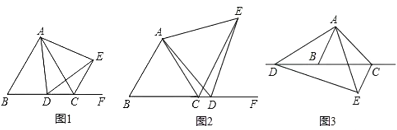
(1)如图①,当点![]() 在边
在边![]() 上时,且点
上时,且点![]() 、点
、点![]() 在
在![]() 同侧,其他条件不变,求证:
同侧,其他条件不变,求证:![]() ;
;
(2)如图②,当点![]() 在边
在边![]() 的延长线上时,且点
的延长线上时,且点![]() 、点
、点![]() 在
在![]() 同侧,其他条件不变,请直接写出线段
同侧,其他条件不变,请直接写出线段![]() ,
,![]() ,
,![]() 之间存在的数量关系,不需证明;
之间存在的数量关系,不需证明;
(3)如图③,当点![]() 在边
在边![]() 的延长线上时,且点
的延长线上时,且点![]() 、点
、点![]() 分别在直线
分别在直线![]() 的异侧,其他条件不变,请直接写出线段
的异侧,其他条件不变,请直接写出线段![]() ,
,![]() ,
,![]() 之间存在的数量关系,不需证明.
之间存在的数量关系,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com