
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
【答案】(1) 乙种小麦长势整齐;(2)![]() .
.
【解析】
试题分析:(1)先分别计算出这两组数据的平均数,再利用方差公式分别求得这两组数据的方差,比较即可得答案;(2)列表(或画树状图)求得所有等可能的结果,利用概率公式求得所抽取的两株配对小麦株高恰好都等于各自平均株高的概率即可.
试题解析:
(1)![]() =(63+66+63+61+64+61)÷6=63.
=(63+66+63+61+64+61)÷6=63.
![]() =(63+65+60+63+64+63)÷6=63.
=(63+65+60+63+64+63)÷6=63.
![]() =
=![]() =3.
=3.
![]() =
=![]() =
=![]() .
.
∵![]() >
>![]() .
.
∴乙种小麦长势整齐.
(2)列表如下
63 | 65 | 60 | 63 | 64 | 63 | |
63 | (63,63) | (63,65) | (63,60) | (63,63) | (63,64) | (63,63) |
66 | (66,63) | (66,65) | (66, 60) | (66,63) | (66,64) | (66,63) |
63 | (63,63) | (63,65) | (63,60) | (63,63) | (63,64) | (63,63) |
61 | (61,63) | (61,65) | (61,60) | (61,63) | (61,64) | (61,63) |
64 | (64,63) | (64,65) | (64,60) | (64,63) | (64,64) | (64,63) |
61 | (61,63) | (61,65) | (61,60) | (61,63) | (61,64) | (61,63) |
∴共有36种情况,其中小麦株高恰好都等于各自平均株高(记为事件A)有6种.
∴P(A)=![]() .
.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】已知点P (3, 2),点Q(3, 2),点R(3, 2),点H(3, 2),下面选项中关于y轴对称的是( ).
A. P和Q B. P和H C. Q和R D. P和R
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
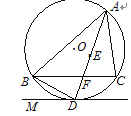
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.
(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF·DA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿直线AB翻折后得到△ABC1 , 再将△ABC绕点A旋转后得到△AB2C2 , 对于下列两个结论: 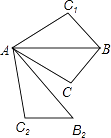
①“△ABC1能绕一点旋转后与△AB2C2重合”;
②“△ABC1能沿一直线翻折后与△AB2C2重合”的正确性是( )
A.结论①、②都正确
B.结论①、②都错误
C.结论①正确、②错误
D.结论①错误、②正确
查看答案和解析>>
科目:初中数学 来源: 题型:
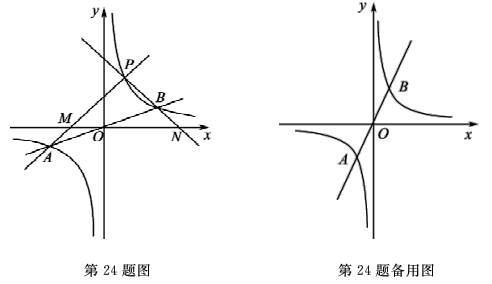
【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数![]() 与
与![]() 的图象性质.小明根据学习函数的经验,对函数
的图象性质.小明根据学习函数的经验,对函数![]() 与
与![]() ,当k>0时
,当k>0时![]() 的图象性质进行了探究,下面是小明的探究过程:
的图象性质进行了探究,下面是小明的探究过程:
(1)如图所示,设函数![]() 与
与![]() 图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .
图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .
(2)若P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下:设P(m,![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则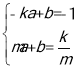 解得
解得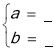
所以,直线PA的解析式为 .
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断ΔPAB的形状,并用k表示出ΔPAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为
的边长为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的动点,连接
上的动点,连接![]() 并延长,交边
并延长,交边![]() 于
于![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,交边
,交边![]() 于点
于点![]() .
.
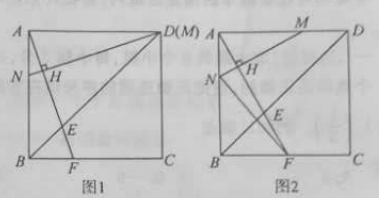
(1)如图1,若点![]() 与点
与点![]() 重合,求证:
重合,求证:![]() ;
;
(2)如图2,若点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,运动时间为
运动,运动时间为![]() .
.
①设![]() ,求
,求![]() 关于t的函数表达式;
关于t的函数表达式;
②当![]() 时,连接
时,连接![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com