
【题目】如图,将△ABC沿直线AB翻折后得到△ABC1 , 再将△ABC绕点A旋转后得到△AB2C2 , 对于下列两个结论: 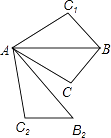
①“△ABC1能绕一点旋转后与△AB2C2重合”;
②“△ABC1能沿一直线翻折后与△AB2C2重合”的正确性是( )
A.结论①、②都正确
B.结论①、②都错误
C.结论①正确、②错误
D.结论①错误、②正确
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 关于某直线对称的两个图形一定能够重合
B. 长方形是轴对称图形
C. 两个全等的三角形一定关于某直线对称
D. 轴对称图形的对称轴至少有一条
查看答案和解析>>
科目:初中数学 来源: 题型:
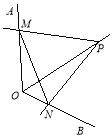
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA,OB相交于M、N两点,则以下结论:(1)PM=PN恒成立,(2)OM+ON的值不变,(3)四边形PMON的面积不变,(4)MN的长不变,其中正确的个数为
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分14分)
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
(1)求直线y=kx+b的解析式;
(2)若点P(x,y)是抛物线y=-x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;
(3)若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值. 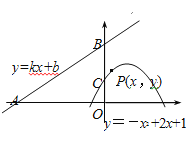
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有21名同学们参加某比赛,预赛成绩各不同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )
A.最高分
B.中位数
C.极差
D.平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com