练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把下列各式因式分解
    （1）4a2﹣16
    （2）（x2+4）2﹣16x2 ．

    【答案】
    （1）解：原式=4（a2﹣4）=4（a+2）（a﹣2）；
    （2）解：原式=（x2+4+4x）（x2+4﹣4x）=（x﹣2）2（x+2）2．
    【解析】（1）原式提取4，再利用平方差公式分解即可；（2）原式利用平方差公式及完全平方公式分解即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水，对居民家庭每户每月用水量采用分档递增收费的方式，每户每月用水量不超过基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费．为对基本用水量进行决策，随机抽查户居民家庭每户每月用水量的数据，整理绘制出下面的统计表：

    （1）为确保%的居民家庭每户每月的基本用水量需求，那么每户每月的基本用水量最低应确定为多少立方米？

    （2）若将（1）中确定的基本用水量及其以内的部分按每立方米元交费，超过基本用水量的部分按每立方米元交费．设表示每户每月用水量（单位：），表示每户每月应交水费（单位：元），求与的函数关系式；

    （3）某户家庭每月交水费是元，请按以上收费方式计算该家庭当月用水量是多少立方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P (3, 2)，点Q(3, 2)，点R(3, 2)，点H(3, 2)，下面选项中关于y轴对称的是（ ）．

    A. P和Q B. P和H C. Q和R D. P和R

    查看答案和解析>>

    科目：初中数学 来源： 题型：

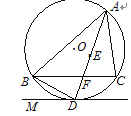
    【题目】（本小题满分10分）

    如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D；连接BD，过点D作直线DM，使∠BDM＝∠DAC．

    （1）求证：直线DM是⊙O的切线；

    （2）求证：DE2＝DF·DA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC沿直线AB翻折后得到△ABC1 ， 再将△ABC绕点A旋转后得到△AB2C2 ， 对于下列两个结论：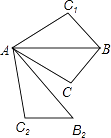
    ①“△ABC1能绕一点旋转后与△AB2C2重合”；
    ②“△ABC1能沿一直线翻折后与△AB2C2重合”的正确性是（ ）
    A.结论①、②都正确
    B.结论①、②都错误
    C.结论①正确、②错误
    D.结论①错误、②正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，BC=AC=4，M为AB中点，D是射线BC上的一动点，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接ED、ME，点D在运动过程中ME的最小值为 ．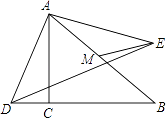

    查看答案和解析>>

    科目：初中数学 来源： 题型：

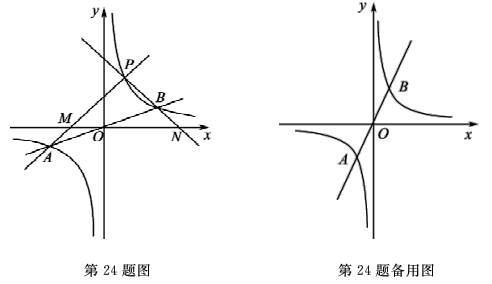
    【题目】有这样一个问题：探究同一坐标系中系数互为倒数的正、反比例函数与的图象性质.小明根据学习函数的经验，对函数与，当k>0时的图象性质进行了探究，下面是小明的探究过程：

    （1）如图所示，设函数与图像的交点为A,B.已知A的坐标为(-k，-1)，则B点的坐标为 .

    (2)若P点为第一象限内双曲线上不同于点B的任意一点.

    ①设直线PA交x轴于点M，直线PB交x轴于点N.求证：PM=PN.

    证明过程如下：设P(m，)，直线PA的解析式为y=ax+b(a≠0).

    则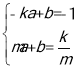 解得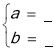

    所以,直线PA的解析式为 ．

    请把上面的解答过程补充完整，并完成剩余的证明.

    ②当P点坐标为(1,k)(k≠1)时，判断ΔPAB的形状，并用k表示出ΔPAB的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若（x﹣2）（x+3）=x2+mx+n，则mn= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．

    例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P为△ABC的自相似点．

    请你运用所学知识，结合上述材料，解决下列问题：

    在平面直角坐标系中，点M是曲线C：上的任意一点，点N是x轴正半轴上的任意一点．

    （1） 如图2，点P是OM上一点，∠ONP=∠M, 试说明点P是△MON的自相似点； 当点M的坐标是，点N的坐标是时，求点P 的坐标；

    （2） 如图3，当点M的坐标是，点N的坐标是时，求△MON的自相似点的坐标；

    （3） 是否存在点M和点N,使△MON无自相似点,？若存在，请直接写出这两点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案