
【题目】正方形![]() 的边长为
的边长为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的动点,连接
上的动点,连接![]() 并延长,交边
并延长,交边![]() 于
于![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,交边
,交边![]() 于点
于点![]() .
.
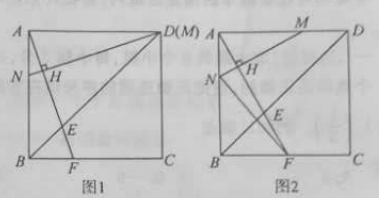
(1)如图1,若点![]() 与点
与点![]() 重合,求证:
重合,求证:![]() ;
;
(2)如图2,若点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,运动时间为
运动,运动时间为![]() .
.
①设![]() ,求
,求![]() 关于t的函数表达式;
关于t的函数表达式;
②当![]() 时,连接
时,连接![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)①![]() ;②5.
;②5.
【解析】
试题分析:(1)根据已知条件易证△ABF≌△NAD,由全等三角形的性质即可得![]() ;(2)
;(2)
先证△ABF∽△NAD,根据全等三角形的性质求得![]() ;(3)利用△ABF∽△NAD,求得t=2,根据(2)的函数解析式求得BF的长,再由勾股定理即可得FN的长.
;(3)利用△ABF∽△NAD,求得t=2,根据(2)的函数解析式求得BF的长,再由勾股定理即可得FN的长.
试题解析:
【解】
(1)∵正方形![]()
∴AD=AB,∠DAN=∠FBA=90°
∵![]()
∴∠NAH+∠ANH=90°
∵∠NDA+∠ANH=90°
∴∠NAH=∠NDA
∴△ABF≌△NAD
∴![]()
(2)①∵正方形![]()
∴AD∥BF
∴∠ADE=∠FBE
∵∠AED=∠BEF
∴△EBF∽△EAD
∴![]()
∵正方形![]()
∴AD=DC=CB=6
∴BD=![]()
∵点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,运动时间为
运动,运动时间为![]() .
.
∴BE=![]() ,DE=
,DE=![]()
∴![]()
∴![]()
②当![]() 时,连接
时,连接![]() ,求
,求![]() 的长.
的长.
∵正方形![]()
∴∠MAN=∠FBA=90°
∵![]()
∴∠NAH+∠ANH=90°
∵∠NMA+∠ANH=90°
∴∠NAH=∠NMA
∴△ABF∽△NAD
∴![]()
∵![]() ,AB=6
,AB=6
∴AN=2,BN=4
∴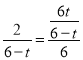
∴t=2
把t=2代入![]() ,得y=3,即BF=3,
,得y=3,即BF=3,
在RT△BFN中,BF=3,BN=4,
根据勾股定理即可得FN=5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有21名同学们参加某比赛,预赛成绩各不同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )
A.最高分
B.中位数
C.极差
D.平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( ) 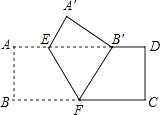
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
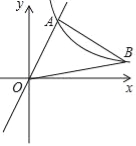
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为 .
,∠AOB=∠OBA=45°,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (a是常数,a≠0),下列结论正确的是( )
(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com