
分析 由判别式的意义得出△=a2+2a+2-4(m+1)≥0对任意的实数a恒成立,解不等式即可.
解答 解:∵关于x的一元二次方程x2+$\sqrt{{a}^{2}+2a+2}$x+(m+1)=0对任意的实数a均有实数根,
∴△=a2+2a+2-4(m+1)≥0对任意的实数a恒成立,
即(a+1)2-(4m+3)≥0,
∴4m+3≤0,
∴m≤-$\frac{3}{4}$.
故答案为m≤-$\frac{3}{4}$.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图所示,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE、BF,试判断△BDF与△CDE全等吗?BF与CE有何位置关系?并说明原因.
如图所示,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE、BF,试判断△BDF与△CDE全等吗?BF与CE有何位置关系?并说明原因.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
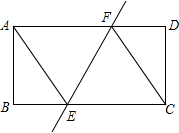 如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF
如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3或$\frac{1}{7}$ | B. | 3或-$\frac{1}{7}$ | C. | 3 | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
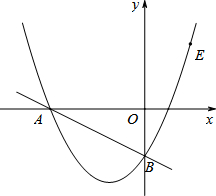 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “明天会下雨”是必然事件 | |
| B. | 想了解“五•一”期间福州市各家庭的消费情况,适合的调查方式是抽样调查 | |
| C. | 正方形是轴对称图形,不是中心对称图形 | |
| D. | 120000用科学记数法表示是1.2×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
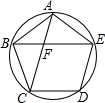 如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.
如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com