
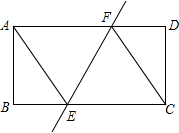
 如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF
如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF分析 (1)根据已知条件判定△ABE≌△CDF,进而证明四边形AECFD的四边相等问题得证;
(2)①在Rt△ABE中,利用勾股定理求出BE的长,即可得到△ABE的周长;
②由①的结论在Rt△ABC中求出EO的长,即可得到结论.
解答 证明:(1)四边形AECF是菱形,
根据对折可知,AF=CF,AE=CE,∠EAF=∠ECF,
∵四边形ABCD是矩形,
∴∠B=∠D,AB=CD
∴△ABE≌△CDF,
∴AE=CF,
∴AE=CE=CF=AF,
∴四边形AECF是菱形;
(2)①连接AC交EF于O,设BE=x,则EC=AE=8-x,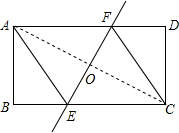
故在Rt△ABE中,(8-x)2=x2+42,
解得x=3,
∴BE=3;
∴AE=5,
∴△ABE的周长=4+3+5=12;
②∵菱形对角线互相平分,
∴AO=CO,
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴AO=2$\sqrt{5}$,
EO2=AE2-AO2=52-(2$\sqrt{5}$)2=5,
∴EO=$\sqrt{5}$,
∴EF=2$\sqrt{5}$.
点评 本题主要考查菱形的判定方法:四条边都相等的四边形是菱形和全等三角形的判定方法以及图形的翻折变换(折叠问题)实质上就是轴对称变换.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | AB⊥BC | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
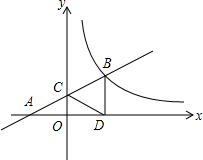 如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.
如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
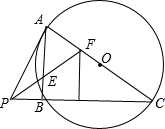 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )| A. | 10 | B. | 12 | C. | $5\sqrt{5}$ | D. | $5\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是菱形,对角线AC与BD相交于点0,∠ACD=30°,BD=2.
如图,四边形ABCD是菱形,对角线AC与BD相交于点0,∠ACD=30°,BD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com