
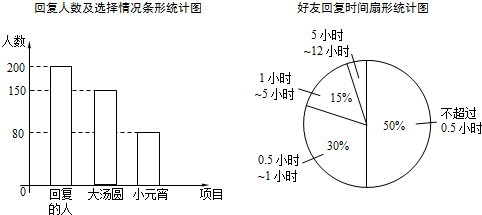
分析 (1)用回复的人数乘以5小时~12小时的人数所占的百分比即可得出答案;
(2)大汤圆的人数加上小元宵的人数减去回复的人数即可得出答案;
(3)用加入“12小时后”这一项的人数除以总人数,再乘以360°即可得出答案.
解答 解:(1)回复时间为5小时~12小时的人数为:200×(1-50%-30%-15%)=10(人);
故答案为:10;
(2)既选择大汤圆,又选择小元宵的人数为:(150+80)-200=30(人)
故答案为:30;
(3)根据题意得:
$\frac{40}{200+40}$×360°=60°.
答:“12小时后”这一项所在扇形的圆心角度数为60°.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
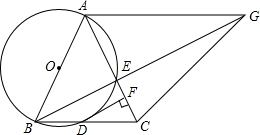 如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
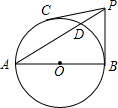 如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.
如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
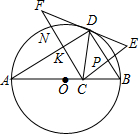 已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:
已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
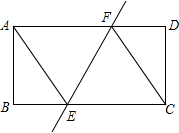 如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF
如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
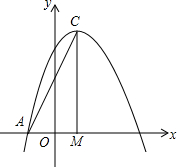 如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.
如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
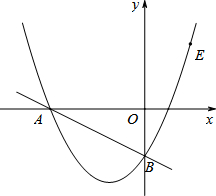 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x-2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com