
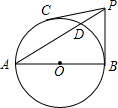
 如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.
如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.分析 (1)如图1中,先证明∠PAB=∠CBA得到$\widehat{AC}$=$\widehat{BD}$,所以∠CDA=∠DAB由此得到CD∥AB即可证明.
(2)如图2中,延长CD交PB于M,PA、BC交于点N,连接ON,先证明ON是△APB的中位线,设OK=a,PK=2a,则BK=$\sqrt{2}$a,BC=2$\sqrt{2}$a,PB=$\sqrt{6}$a,利用勾股定理求出CM、PM即可解决问题.
解答 (1)证明: 如图1中,连接AC、BD、PO.
如图1中,连接AC、BD、PO.
∵PB、PC是切线,
∴∠OPC=∠OPB,PC=PB,
∴PO垂直平分BC,KC=KB,
∵∠OPB+∠PBK=90°,∠PBK+∠OBK=90°,
∴∠OBK=∠OPB,
∵∠BPC=2∠PAB,
∴∠OBK=∠PAB,
∴$\widehat{AC}$=$\widehat{BD}$,
∴∠CDA=∠DAB,
∴CD∥AB,
∵AB⊥PB,
∴CD⊥PB.
(2) 如图2中,延长CD交PB于M,PA、BC交于点N,连接ON,
如图2中,延长CD交PB于M,PA、BC交于点N,连接ON,
由(1)可知∠NAB=∠NBA,
∴NA=NB,
∵AO=OB,
∴NO⊥AB,∵PB⊥AB,
∴ON∥PB,ON=$\frac{1}{2}$PB,
∴$\frac{OK}{PK}$=$\frac{ON}{PB}$=$\frac{1}{2}$,设OK=a,PK=2a,则BK=$\sqrt{2}$a,BC=2$\sqrt{2}$a,PB=$\sqrt{6}$a,
∵$\frac{1}{2}$•BC•PK=$\frac{1}{2}$•PB•CM,
∴CM=$\frac{BC•PK}{PB}$=$\frac{4\sqrt{3}}{3}$a,
∴BM=$\sqrt{B{C}^{2}-C{M}^{2}}$=$\sqrt{(2\sqrt{2}a)^{2}-(\frac{4\sqrt{3}}{3}a)^{2}}$=$\frac{2\sqrt{6}}{3}$a,
∴PM=PB-BM=$\frac{\sqrt{6}}{3}$a,
∴tan∠PCD=$\frac{PM}{CM}$=$\frac{\frac{\sqrt{6}}{3}a}{\frac{4\sqrt{3}}{3}a}$=$\frac{\sqrt{2}}{4}$.
点评 本题考查切线的性质、圆的有关性质、等腰三角形的性质、三角形中位线定理勾股定理等知识,第一问解题的关键是证明CD∥AB,第二问解题的关键是三角形中位线定理灵活运用,设未知数求出相应的线段,属于中考压轴题,有一定的难度.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
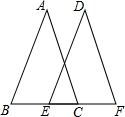 如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )
如图所示,AB=DE,AC=DF,BC=EF,小雪根据这些条件得出了四个结论,你认为叙述正确的个数是:(1)AB∥DE;(2)AC∥DF;(3)BE=CF;(4)∠DEF=∠ACB.( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
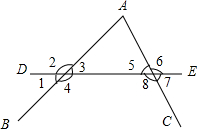 如图,直线DE截AB,AC,构成八个角:
如图,直线DE截AB,AC,构成八个角:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com