
分析 利用乘法分配律和无理数的乘法($\sqrt{3}$($\sqrt{3}$-$\frac{1}{\sqrt{3}}$)=3-1),取绝对值符号|$\sqrt{3}$-2|=2-$\sqrt{3}$,计算即可
解答 解:$\sqrt{1}$+|$\sqrt{3}$-2|+$\sqrt{3}$($\sqrt{3}$-$\frac{1}{\sqrt{3}}$)-$\root{3}{-8}$
=1+2-$\sqrt{3}$+$\sqrt{3}$×$\sqrt{3}$-$\sqrt{3}$×$\frac{1}{\sqrt{3}}$-(-2)
=1+2-$\sqrt{3}$+3-1+2
=7-$\sqrt{3}$.
点评 此题是实数的运算,主要考查了算术平方根的一样,立方根的意义,取绝对值,以及无理数的乘法,解本题的关键是取绝对值和无理数的乘法.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:解答题
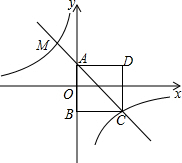 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
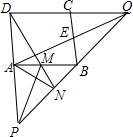 如图,在正方形ABcD中,M为AB中点,连结DM并延长DM到N,使NA2=NM•ND.
如图,在正方形ABcD中,M为AB中点,连结DM并延长DM到N,使NA2=NM•ND.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
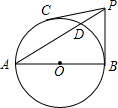 如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.
如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证:
如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
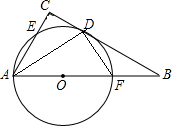
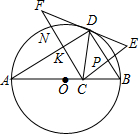 已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:
已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com