
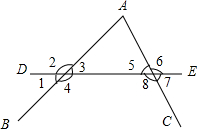
 如图,直线DE截AB,AC,构成八个角:
如图,直线DE截AB,AC,构成八个角:分析 (1)根据两直线被第三条直线所截,两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角是同位角,可得同位角;两个角在截线的两侧,被截两直线的中间的角是内错角,可得内错角;两个角在截线的同侧,被截两直线的中间的角是同旁内角,可得同旁内角;
(2)根据三线八角中同位角、内错角或同旁内角的定义进行解答.
解答 解:(1)同位角有:∠2与∠5,∠3与∠6,∠4与∠7,∠1与∠8;
内错角有:∠3与∠8,∠4与∠5;
同旁内角有:∠3与∠5,∠4与∠8;
(2)∠A和∠5是直线AC截直线DE、AB形成的同旁内角;
∠A和∠6是直线AC截直线DE、AB形成的内错角;
∠A和∠8是直线AC截直线DE、AB形成的同位角.
点评 本题考查了同位角、内错角,同旁内角,关键是掌握同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
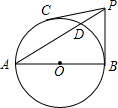 如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.
如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
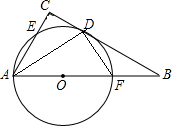 如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证:
如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
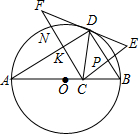 已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:
已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.
如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com