
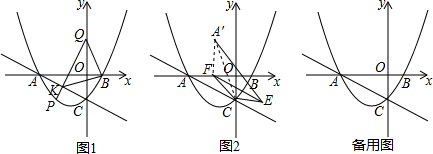
���� ��1�����ݶԳ��x=$-\frac{b}{2a}$������������ߵĶԳ��ᣬȻ����x=0��y=-$\sqrt{3}$������OC=$\sqrt{3}$����y=0�ã�$\frac{\sqrt{3}}{3}{x}^{2}+\frac{2\sqrt{3}}{3}x-\sqrt{3}=0$������AB=4�����������ε������ʽ���㼴�ɣ�
��2����ͼ1��ʾ����Rt��AOC��Rt��OBC�У���������������Ǻ���ֵ��֪��á�ABC=60�㣬��BCO=30�㣬�Ӷ��õ���ACB=90�㣬�ӳ�BC��B��ʹB��C=BC������QB�佻AC�ڵ�K����ʱ��BQK�ܳ���С��������ԳƵ����ʿ�֪��B�������Ϊ��-1��-2$\sqrt{3}$����Ȼ������ֱ��QB��Ľ���ʽΪy=3$\sqrt{3}x+\sqrt{3}$��Ȼ��y=3$\sqrt{3}x+\sqrt{3}$��y=$\frac{\sqrt{3}}{3}{x}^{2}+\frac{2}{3}\sqrt{3}x-\sqrt{3}$����ɷ��������õ�P�����꣬�����Rt��OBQ��Rt��MB��Q�У����ù��ɶ������QB����QB���ȼ�����á�BQK����Сֵ��
��3��������ͼ3��ʾ���ӳ�CF��A��A���M���ڡ�ACO�У��ɹ��ɶ�����ã�AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=2$\sqrt{3}$���Ӷ��õ���A�������Ϊ��0��$\sqrt{3}$����Ȼ�����е����깫ʽ����õ�M������Ϊ��$-\frac{3}{2}$��$\frac{\sqrt{3}}{2}$������ֱ��FC�Ľ���ʽΪy=kx-$\sqrt{3}$������M�������������ֱ��FC�Ľ���ʽΪy=-$\sqrt{3}x-\sqrt{3}$����y=0�ɽ�õ�F������Ϊ��-1��0����
����ͼ4��ʾ��֤���ı���OCEA��Ϊ���Σ��Ӷ�����õ�F��AA����е㣬�Ӷ�����õ�F�����ꣻ����ͼ5��ʾ���ɷ��۵����ʿ�֪��CF��AA�䣬�����AC�Ľ���ʽ���������ֱ����ֱ�ߵ�һ����ϵ���ij˻�Ϊ-1�������CF�Ľ���ʽ���Ӷ�����õ�F�����ꣻ����ͼ6��ʾ���ӳ�FC��AA���ڵ�N�������ֱ��AA��Ľ���ʽ���������ֱ����ֱ�ߵ�һ����ϵ���ij˻�Ϊ-1�������CF�Ľ���ʽ���Ӷ�����õ�F�����꣮
��� �⣺��1���Գ��x=$-\frac{b}{2a}$=-$\frac{\frac{2\sqrt{3}}{3}}{2��\frac{\sqrt{3}}{3}}$=-1��
��x=0��y=-$\sqrt{3}$��
���Ե�C������Ϊ��0��-$\sqrt{3}$����
��y=0�ã�$\frac{\sqrt{3}}{3}{x}^{2}+\frac{2\sqrt{3}}{3}x-\sqrt{3}=0$��
��ã�x1=-3��x2=1��
��A��B���������ֱ�Ϊ��-3��0������1��0����
��AB=4��OC=$\sqrt{3}$��
���ABC�����=$\frac{1}{2}��AB•OC$=$\frac{1}{2}��4��\sqrt{3}$=2$\sqrt{3}$��
��2����ͼ1��ʾ��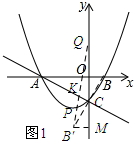
��Rt��AOC��tan��ACO=$\frac{AO}{CO}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$����Rt��OBC��tan��BCO=$\frac{OB}{OC}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$��
���ABC=60�㣬��BCO=30�㣮
���ACB=90�㣮
�ӳ�BC��B��ʹB��C=BC������QB�佻AC�ڵ�K����ʱ��BQK�ܳ���С��
�ߵ�B���B�������AC�Գƣ�
���Ե�B�������Ϊ��-1��-2$\sqrt{3}$����
��B��Q�Ľ���ʽΪy=kx+b����
$\left\{\begin{array}{l}{-k+b=-2\sqrt{3}}\\{b=\sqrt{3}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=3\sqrt{3}}\\{b=\sqrt{3}}\end{array}\right.$��
����ֱ��QB��Ľ���ʽΪy=3$\sqrt{3}x+\sqrt{3}$��
��������ã�3$\sqrt{3}x+\sqrt{3}$=$\frac{\sqrt{3}}{3}{x}^{2}+\frac{2}{3}\sqrt{3}x-\sqrt{3}$����ã�${x}_{1}=\frac{7-\sqrt{73}}{2}$��${x}_{2}=\frac{7+\sqrt{73}}{2}$����ȥ����
��x=$\frac{7-\sqrt{73}}{2}$����y=3$\sqrt{3}x+\sqrt{3}$�ã�y=$\frac{23\sqrt{3}-3\sqrt{219}}{2}$��
���P��������$\frac{7-\sqrt{73}}{2}$��$\frac{23\sqrt{3}-3\sqrt{219}}{2}$��
��Rt��OBQ��QB=$\sqrt{O{Q}^{2}+0{B}^{2}}=\sqrt{��\sqrt{3}��^{2}+{1}^{2}}$=2����Rt��MB��Q��QB��=$\sqrt{Q{M}^{2}+B��{M}^{2}}$=$\sqrt{��3\sqrt{3}��^{2}+{1}^{2}}$=2$\sqrt{7}$��
��BQK���ܳ�=QB+QK+KB=QB��+QB=2+2$\sqrt{7}$��
��3������ͼ3��ʾ���ӳ�CF��A��A���M��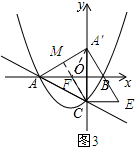
�ڡ�ACO�У��ɹ��ɶ����ã�AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=2$\sqrt{3}$��
�ɷ��۵����ʿ�֪AC=A��C=2$\sqrt{3}$��
���A���������0��$\sqrt{3}$����
���M��������$-\frac{3}{2}$��$\frac{\sqrt{3}}{2}$����
��ֱ��FC�Ľ���ʽΪy=kx-$\sqrt{3}$������M���������ã�-$\frac{3}{2}$k-$\sqrt{3}$=$\frac{\sqrt{3}}{2}$��
��ã�k=-$\sqrt{3}$��
��ֱ��FC�Ľ���ʽΪy=-$\sqrt{3}x-\sqrt{3}$��
��y=0�ã�-$\sqrt{3}x-\sqrt{3}=0$��
��ã�x=-1��
���F��������-1��0����
����ͼ4��ʾ��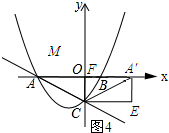
�ߡ�A��EC=90�㣬
���EA��F=��A��OC=��A��EC=90�㣮
���ı���OCEA���Ǿ��Σ�
��CE=OA��=OA��
���F��AA����е㣮
���F��������0��0����
����ͼ5��ʾ������A��C��A����ͬһ��ֱ����ʱ��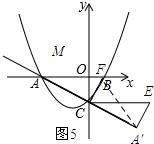
�ɷ��۵����ʿ�֪��CF��AA�䣮
��AC�Ľ���ʽΪy=kx-$\sqrt{3}$������A���������ã�-3k-$\sqrt{3}$=0��
��ã�k=$-\frac{\sqrt{3}}{3}$��
��CF��AC��
��ֱ��CF�Ľ���ʽΪy=$\sqrt{3}x-\sqrt{3}$��
��y=0����ã�x=1��
���F��������1��0����
����ͼ6��ʾ���ӳ�FC��AA���ڵ�N��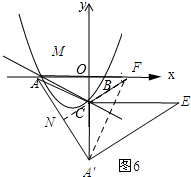
�ɷ��۵����ʿ�֪��CF��AA�䣬AN=A��N��AC=A��C=2$\sqrt{3}$��
���A���������0��-3$\sqrt{3}$����
�ɵ�A�͵�A��������֪����N������Ϊ��$-\frac{3}{2}$��$-\frac{3\sqrt{3}}{2}$����
��ֱ��CF�Ľ���ʽΪy=kx-$\sqrt{3}$������N���������ã�$-\frac{3}{2}k-\sqrt{3}=-\frac{3\sqrt{3}}{3}$��
��ã�k=$\frac{\sqrt{3}}{3}$��
��CF�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}x-\sqrt{3}$��
��y=0�ã�$\frac{\sqrt{3}}{3}x-\sqrt{3}=0$��
��ã�x=3��
���F��������3��0����
������������F��������-1��0����0��0����1��0����3��0����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˶��κ�����ͼ������ʡ�һ�κ�����ͼ������ʣ����������ε����ʺ��ж������۵����ʡ����ɶ����ͽ�һԪ���η��̵�֪ʶ�㣬�ҳ���BQK�ܳ���С�͡�CEA����ֱ�������ε��������Ӷ�����ͼ���ǽ���Ĺؼ���


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
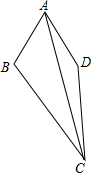 ��ͼ���ı���ABCD�У���BAD=60�㣬��BCD=30�㣬AB=AD��BC=8cm��CD=5cm����AC�ij�Ϊ$\sqrt{89}$cm��
��ͼ���ı���ABCD�У���BAD=60�㣬��BCD=30�㣬AB=AD��BC=8cm��CD=5cm����AC�ij�Ϊ$\sqrt{89}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
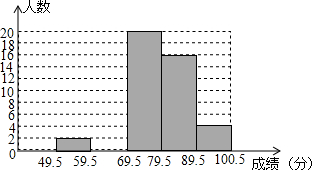 ��У�������ڼ䣬��չ�ˡ�������������質�������ڳ����У�ѧ�����Գ����ɼ�����ͳ�Ʒ��������Ƴ�����Ƶ����Ƶ�ʷֲ�����Ƶ���ֲ�ֱ��ͼ����ͼ�����������ͼ���ṩ����Ϣ������������⣺
��У�������ڼ䣬��չ�ˡ�������������質�������ڳ����У�ѧ�����Գ����ɼ�����ͳ�Ʒ��������Ƴ�����Ƶ����Ƶ�ʷֲ�����Ƶ���ֲ�ֱ��ͼ����ͼ�����������ͼ���ṩ����Ϣ������������⣺| ���� | 74.5��79.5 | 79.5��84.5 | 84.5��89.5 | 89.5��94.5 | 94.5��100.5 | �ϼ� |
| Ƶ�� | 2 | a | 20 | 16 | 4 | 50 |
| Ƶ�� | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
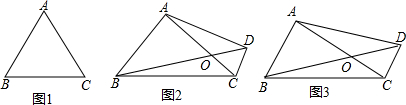
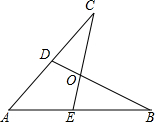 ��ͼ��ʾ��E��D��AB��AC�ϵ����㣬BD��CE���ڵ�O����AB=AC��ʹ��ACE�ա�ABD���㲹���������AD=AE��CD=BE���B=��C���ADB=��AEC��
��ͼ��ʾ��E��D��AB��AC�ϵ����㣬BD��CE���ڵ�O����AB=AC��ʹ��ACE�ա�ABD���㲹���������AD=AE��CD=BE���B=��C���ADB=��AEC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com