
分析 如果设有x辆车,则有(5x+15)吨货物.根据若每辆汽车装满10吨,则最后一辆汽车不满也不空,列出不等式组,再求解,又因为车必须是整数,进而可得出结论.
解答 解:设共有x辆汽车,
由题意有$\left\{\begin{array}{l}{10(x-1)<5x+15}\\{5x+15<10x}\end{array}\right.$,
解得3<x<5.
∵x为正整数,
∴x=4,
∴5x+15=5×4+15=35.
所以,这批香蕉共有35吨.
点评 本题考查了一元一次不等式组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的数量关系.理解“每辆汽车只装5吨,则剩下15吨香蕉;若每辆汽车装满10吨,则最后一辆汽车不满也不空”这句话中包含的不等关系是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
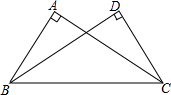 如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDB,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.
如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDB,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交 | B. | 外切 | C. | 内切 | D. | 外离 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
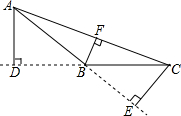 如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )
如图所示,AD、CE、BF是△ABC的三条高,AB=5,BC=4,AD=3,则CE=( )| A. | $\frac{12}{5}$ | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com