
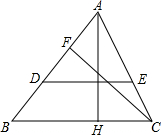
 如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF.
如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF. 分析 利用已知条件易证△ABH∽△CBF,由相似三角形的性质可得:AH:AB=CF:BC,因为AD=AH,所以AD:AB=CF:BC,再由DE∥BC,可得AD:AB=DE:BC,所以DE:BC=CF:BC,进而可证明:DE=CF.
解答 证明:∵AH⊥BC,CF⊥AB,
∴∠AHB=∠CFB=90°,
∵∠ABH=∠CBF,
∴△ABH∽△CBF,
∴AH:AB=CF:BC,
∵AD=AH,
∴AD:AB=CF:BC,
∵DE∥BC,
∴AD:AB=DE:BC,
∴DE:BC=CF:BC,
∴DE=CF.
点评 本题考查了相似三角形的判定和性质以及平行线分线段成比例定理的运用,解题的关键是利用相似和平行线分线段成比例定理分别得到AH:AB=CF:BC和AD:AB=DE:BC,由比例的性质即可得到DE=CF.


科目:初中数学 来源: 题型:填空题
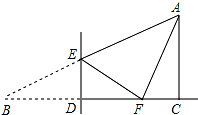 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
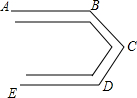 要修建一条如图所示的公路,AB∥DE,∠D=120°,为保证汽车的行驶安全,在C处拐弯的角度∠BCD不能低于100°,求在B处拐弯的角度最大是多少?
要修建一条如图所示的公路,AB∥DE,∠D=120°,为保证汽车的行驶安全,在C处拐弯的角度∠BCD不能低于100°,求在B处拐弯的角度最大是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
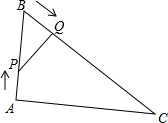 如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.
如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com