
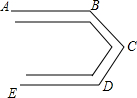
 要修建一条如图所示的公路,AB∥DE,∠D=120°,为保证汽车的行驶安全,在C处拐弯的角度∠BCD不能低于100°,求在B处拐弯的角度最大是多少?
要修建一条如图所示的公路,AB∥DE,∠D=120°,为保证汽车的行驶安全,在C处拐弯的角度∠BCD不能低于100°,求在B处拐弯的角度最大是多少? 科目:初中数学 来源: 题型:选择题
| A. | 缩小为原来的$\frac{1}{2}$ | B. | 缩小为原来的$\frac{1}{4}$ | C. | 分式的值不变 | D. | 扩大为原来的2倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 比赛日期 | 2012-8-4 | 2013-5-21 | 2014-9-28 | 2015-5-20 | 2015-5-31 |
| 比赛地点 | 英国伦敦 | 中国北京 | 韩国仁川 | 中国北京 | 美国尤金 |
| 成绩(秒) | 10.19 | 10.06 | 10.10 | 10.06 | 9.99 |
| A. | 10.06秒,10.06秒 | B. | 10.10秒,10.06秒 | C. | 10.06秒,10.08秒 | D. | 10.08秒,10.06秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
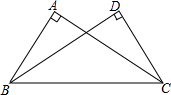 如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDB,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.
如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDB,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com