
分析 (1)把5拆为($\sqrt{2}$)2+($\sqrt{3}$)2,然后利用完全平方公式进行解答;
(2)把11拆为($\sqrt{5}$)2+($\sqrt{6}$)2,把7拆为($\sqrt{2}$)2+($\sqrt{5}$)2,然后利用完全平方公式进行解答;
(3)先配成完全平方式,再根据二次根式的性质化简计算即可.
解答 解:(1):5+2$\sqrt{6}$=2+3+2$\sqrt{6}$=($\sqrt{2}$)2+($\sqrt{3}$)2+2$\sqrt{6}$=($\sqrt{2}$+$\sqrt{3}$)2.
5-2$\sqrt{6}$=2+3-2$\sqrt{6}$=($\sqrt{2}$)2+($\sqrt{3}$)2-2$\sqrt{6}$=($\sqrt{2}$-$\sqrt{3}$)2.
故答案是:$\sqrt{2}$+$\sqrt{3}$;$\sqrt{2}$-$\sqrt{3}$;
(2)$\sqrt{11-2\sqrt{30}}+\sqrt{7-2\sqrt{10}}$,
=$\sqrt{(\sqrt{5}-\sqrt{6})^{2}}$+$\sqrt{(\sqrt{2}-\sqrt{5})^{2}}$,
=$\sqrt{6}$-$\sqrt{5}$+$\sqrt{5}$-$\sqrt{2}$,
=$\sqrt{6}$-$\sqrt{2}$;
(3)∵1≤x≤2,
∴$\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}$,
=$\sqrt{(\sqrt{x-1}+1)^{2}}$+$\sqrt{(\sqrt{x-1}-1)^{2}}$,
=$\sqrt{x-1}$+1+1-$\sqrt{x-1}$,
=2.
点评 本题考查了配方法的应用,二次根式的化简求值.解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.


科目:初中数学 来源: 题型:解答题
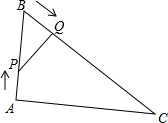 如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.
如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
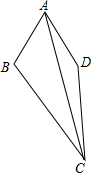 如图,四边形ABCD中,∠BAD=60°,∠BCD=30°,AB=AD,BC=8cm,CD=5cm,则AC的长为$\sqrt{89}$cm.
如图,四边形ABCD中,∠BAD=60°,∠BCD=30°,AB=AD,BC=8cm,CD=5cm,则AC的长为$\sqrt{89}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:-2-2-$\sqrt{(-\frac{1}{2})^{2}}$+(π-3.14)0.
(1)计算:-2-2-$\sqrt{(-\frac{1}{2})^{2}}$+(π-3.14)0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
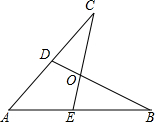 如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
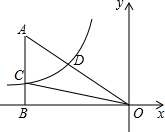 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )| A. | -4 | B. | -6 | C. | -9 | D. | -12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com