
 中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.分析 (1)由题意得,我海监船与不明渔船行驶距离相等,即在OA上找到一点,使其到A点与B点的距离相等,所以连接AB,作AB的垂直平分线即可.
(2)连接BC,利用第(1)题中作图,可得BC=AC.在直角三角形BOC中,利用勾股定理列出方程122+(36-BC)2=BC2,解方程即可.
解答 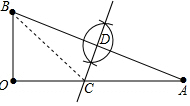 解:(1)作AB的垂直平分线与OA交于点C;
解:(1)作AB的垂直平分线与OA交于点C;
(2)连接BC,
由作图可得:CD为AB的中垂线,则CB=CA.
由题意可得:OC=36-CA=36-CB.
∵OA⊥OB,
∴在Rt△BOC中,BO2+OC2=BC2,
即:122+(36-BC)2=BC2,
解得BC=20.
答:我国海监船行驶的航程BC的长为20海里.
点评 本题考查了勾股定理的应用以及线段垂直平分线的性质,利用勾股定理不仅仅能求直角三角形的边长,而且它也是直角三角形中一个重要的等量关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在长为100m,宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为( )
如图,在长为100m,宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为( )| A. | 100×80-100x-80x=7644 | B. | (100-x)(80-x)+x2=7644 | ||
| C. | (100-x)(80-x)=7644 | D. | 100x+80x-x2=7644 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在宽为24m的马路两侧各竖立两根相同高度的灯杆AB、CD.当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长NE=2m,试确定小明离路灯CD的距离.
如图,在宽为24m的马路两侧各竖立两根相同高度的灯杆AB、CD.当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长NE=2m,试确定小明离路灯CD的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
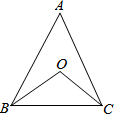 如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 2α° | B. | (α+60)° | C. | (α+90)° | D. | ($\frac{1}{2}$α+90)° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com