
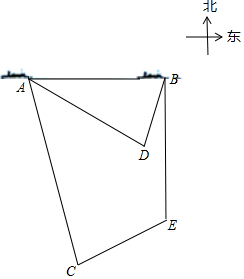
 如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方.
如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方.分析 (1)根据已知条件得到∠BAE=∠EAF=45°,∠ABE=90°,求得∠BEA=45°,于是得到结论;
(2)根据三角函数的定义得到$\frac{BE}{AE}$=$\frac{\sqrt{2}}{2}$=$\frac{AD}{AC}$,根据已知条件得到∠DAC=∠DAF-∠CAF=45°,求得∠BAD=∠EAC,根据相似三角形的性质即可得到结论.
解答 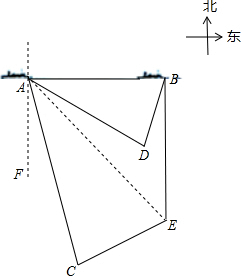 解:(1)∵岛E在A处东南方向,
解:(1)∵岛E在A处东南方向,
∴∠BAE=∠EAF=45°,
∵E恰好在B的正南方.
∴∠ABE=90°,
∴∠BEA=45°,
∴AB=EB,
∴船航行的距离AB正好是岛E离开B处的距离;
(2)∵∠ABE=90°∠BAE=45°,
∴sin∠BAE=$\frac{BE}{AE}$=$\frac{\sqrt{2}}{2}$=$\frac{AD}{AC}$,
∵∠CAF=15°,∠DAF=60°,
∴∠DAC=∠DAF-∠CAF=45°,
∴∠BAE-∠DAE=∠DAC-∠DAE,
即∠BAD=∠EAC,
∴△BAD∽△EAC,
∴$\frac{BD}{EC}$=$\frac{AD}{AC}$=$\frac{\sqrt{2}}{2}$,
∵BD=18海里,
∴CE=18$\sqrt{2}$海里.
点评 此题考查了方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 对某地区现有的16名百岁以上老人睡眠时间的调查 | |
| B. | 对“神舟十一号”运载火箭发射前零部件质量情况的调查 | |
| C. | 对某校九年级三班学生视力情况的调查 | |
| D. | 对某市场上某一品牌电脑使用寿命的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.
如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系?
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
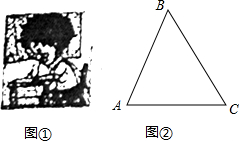 推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
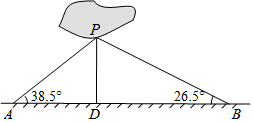 如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)
如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com