
 如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.
如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$. 分析 连接OC、AE,OC的反向延长线交AE于E,如图,利用圆周角定理得到∠ACB=∠AEB=90°,则AB=2$\sqrt{5}$,再根据切线的性质得OC⊥PC,接着证明△PCB∽△PAC,利用相似比得到PC=2PB,PC2=PB•PA,则4PB2=PB(PB+2$\sqrt{5}$),解得PB=$\frac{2\sqrt{5}}{3}$,接下来利用等腰三角形的性质得CH⊥AE,则PC∥AE,所以∠P=∠PAE,然后证明Rt△ABE∽Rt△POC,则利用相似比可求出BE的长.
解答 解:连接OC、AE,OC的反向延长线交AE于E,如图,
∵AB为直径,
∴∠ACB=∠AEB=90°,
在Rt△ACB中,AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵PC为切线,
∴OC⊥PC,
∴∠PCO=90°,即∠OCB+∠PCB=90°,
而∠OCB+∠ACO=90°,
∴∠OCA=∠PCB,
而OCA=∠OAC,
∴∠OCA=∠PCB,
而∠CPB=∠APC,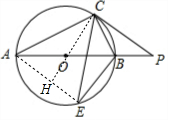
∴△PCB∽△PAC,
∴$\frac{PC}{PA}$=$\frac{PB}{PC}$=$\frac{BC}{AC}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴PC=2PB,PC2=PB•PA,
∴4PB2=PB(PB+2$\sqrt{5}$),解得PB=$\frac{2\sqrt{5}}{3}$,
∴OP=OB+PB=$\frac{5\sqrt{5}}{3}$,
∵CA=CE,
∴CH⊥AE,
∴PC∥AE,
∴∠P=∠PAE,
∴Rt△ABE∽Rt△POC,
∴$\frac{BE}{OC}$=$\frac{AB}{PO}$,即$\frac{BE}{\sqrt{5}}$=$\frac{2\sqrt{5}}{\frac{5\sqrt{5}}{3}}$,
∴BE=$\frac{6\sqrt{5}}{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了相似三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
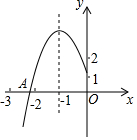 如图所示,抛物线y=ax2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和(-2,0)之间,以下结论:
如图所示,抛物线y=ax2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和(-2,0)之间,以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
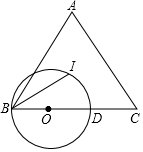 如图,△ABC中,AC=BC,I为△ABC的内心,⊙O经过B,I两点,且O在BC边上,⊙O与BC交于点D.
如图,△ABC中,AC=BC,I为△ABC的内心,⊙O经过B,I两点,且O在BC边上,⊙O与BC交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,BC=AC=4,∠C=90°,在平面内,△ABC绕点A逆时针旋转α,对应得△AB′C′,以B′C′为直径的圆第一次与直线AB相切时.若B′C′中点为O,过O作OH⊥AB交AB′于点G,则S△B′OG=$\frac{8}{7}$.
如图,在△ABC中,BC=AC=4,∠C=90°,在平面内,△ABC绕点A逆时针旋转α,对应得△AB′C′,以B′C′为直径的圆第一次与直线AB相切时.若B′C′中点为O,过O作OH⊥AB交AB′于点G,则S△B′OG=$\frac{8}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
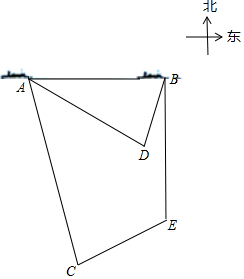 如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方.
如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
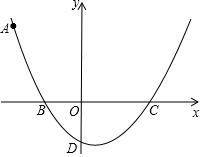 如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).
如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com