
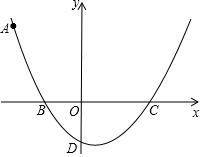
 如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).
如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).分析 (1)根据点A(-4,4),D(0,-2)在抛物线y=$\frac{1}{k}$(x+2)(x+a)上,列方程组即可得到结论;
(2)过E作EM⊥x轴于M,根据余角的性质得到∠CEM=∠EBC,设点E的横坐标为c,则M(c,0),当y=0时,$\frac{1}{4}$(x+2)(x-4)=0解方程得到B(-2,0),C(4,0),OB=2,OC=4,在Rt△CEM和Rt△EBM内,根据三角函数的定义即可得到结论;
(3)过P作PW⊥y轴于W,根据点W,P的纵坐标为$\frac{1}{4}$(t+2)(t-4)列方程即可得到结论.
解答 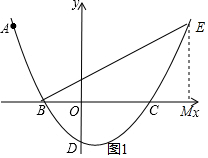 解:(1)∵点A(-4,4),D(0,-2)在抛物线y=$\frac{1}{k}$(x+2)(x+a)上,
解:(1)∵点A(-4,4),D(0,-2)在抛物线y=$\frac{1}{k}$(x+2)(x+a)上,
∴$\left\{\begin{array}{l}{4k=8-2}\\{-2k=2a}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-4}\\{k=4}\end{array}\right.$;
(2)如图1,过E作EM⊥x轴于M,∠BCE=90°+CEM,
∵∠BCE=90°+∠EBC,
∴∠CEM=∠EBC,
设点E的横坐标为c,则M(c,0),点E的纵坐标为$\frac{1}{4}$(c+2)(c-4),
∵点E是第一象限抛物线上一点,
∴OM=c,EM=$\frac{1}{4}$(c+2)(c-4),抛物线y=$\frac{1}{4}$(x+2)(x-4)交x轴负半轴于点B,交x轴正半轴于点C,
当y=0时,$\frac{1}{4}$(x+2)(x-4)=0
∴x1=4,x2=-2,
∴B(-2,0),C(4,0),
∴OB=2,OC=4,
在Rt△CEM和Rt△EBM内,tan∠CEM=$\frac{MC}{EM}$,tan∠EBM=$\frac{EM}{BM}$,∠CEM=∠EMB,
∴$\frac{MC}{EM}$=$\frac{EM}{BM}$,
∵MC=OM-OC=c-4,BM=OM+OB=c+2,
∴$\frac{c-4}{\frac{1}{4}(c+2)(c-4)}$=$\frac{\frac{1}{4}(c+2)(c-4)}{c+2}$,
∵点E在第一象限,
∴c-4≠0,c+2≠0,
∴(c-4)(c+2)=16,
解得:c1=6,c2=-4(舍去),
∴E(6,4);
(3)在Rt△GHT内,HT=$\sqrt{2}$GH=2FH
EH=HTE=3FH,
∴tan∠HEF=$\frac{1}{3}$,
∵∠DFP=90°-∠HFE=∠FEH,
∴tan∠DFP=$\frac{1}{3}$,
过P作PW⊥y轴于W,
∴点W,P的纵坐标为$\frac{1}{4}$(t+2)(t-4),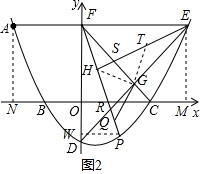
∵点P在第四象限,
∴OW=$\frac{1}{4}$(t+2)(t-4),
∴FW=OF+OW=4-$\frac{1}{4}$(t+2)(t-4),
∴tan∠WFP=$\frac{PW}{FW}=\frac{1}{3}$,
∴FW=3PW,4-$\frac{1}{4}$(t+2)(t-4)=3t,
解得:t1=2,t2=-12,(舍去),
∴t=2时,GQ=$\sqrt{2}$FH.
点评 本题考查了待定系数法求函数的解析式,抛物线与x轴的交点,解直角三角形,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.
如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
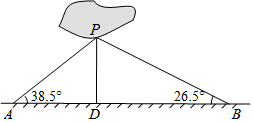 如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)
如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 矩形的对角线互相垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com