
如图,△ABC中,∠BAC=90°,AB=AC,边BA绕点B顺时针旋转α角得到线段BP,连结PA,PC,过点P作PD⊥AC于点D.
(1)如图1,若α=60°,求∠DPC的度数;
(2)如图2,若α=30°,直接写出∠DPC的 度数;
度数;
(3)如图3,若α=150°,依题意补全图,并求∠DPC的度数.

.解:
(1)∵边BA绕点B顺时针旋转α角得到线段BP,
∴BA= BP,
∵α=60°,∴△ABP是等边三角形,.
∴∠BAP=60º,AP= AC,
又∵∠BAC=90°,
∴∠PAC=30º,∠ACP=75º,
 ∵PD⊥AC于点D,
∵PD⊥AC于点D,
∴∠DPC=15º.. (2)结论:∠DPC=75º
(3) 画图.
画图.
过点A作AE⊥BP于E.
∴∠AEB=90º,
∵∠ABP=150°,∴∠1=30º,∠BAE=60º,
 又∵BA= BP,
又∵BA= BP,
∴∠2=∠3=15º,
∴∠PAE=75º,
∵∠BAC=90°,
∴∠4=75º,
∴∠PAE=∠4,
∵PD⊥AC于点D,
∴∠AEP=∠ADP =90º,
∴△APE≌△APD, ∴AE= AD,
在Rt△ABE中,∠1=30º,∴ ,
,
又∵AB=AC,
∴ ,
,
∴AD=CD,
又∵∠ADP=∠CDP=90º,
∴△ ADP≌△CDP, ∴∠DCP=∠4=75º,
∴∠DPC=15º 另法:作平行,构造平行四边形.
 | |||
 | |||


科目:初中数学 来源: 题型:
数学活动课上,老师提出这样一个问题:如果AB=BC,∠ABC=60°,∠APC=30°,连接
PB,那么PA、PB、PC之间会有怎样的等量关系呢?
经过思考后,部分同学进行了如下的交流:
小蕾:我将图形进行了特殊化,让点P在BA延长线上(如图1),得到了一个猜想:
PA2+PC2=PB2 .
小东:我假设点P在∠ABC的内部,根据题目条件,这个图形具有“共端点等线段”的特点,可以利用旋转解决问题,旋转△PAB 后得到△P′CB ,并且可推出△PBP′ ,△PCP′ 分别是等边三角形、直角三角形,就能得到猜想和证明方法.
这时老师对同学们说,请大家完成以下问题:
(1)如图2,点P在∠ABC的内部,
①PA=4,PC= ,PB= .
,PB= .
②用等式表示PA、PB、PC之间的数量关系,并证明.
 (2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
(2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
|
|

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系 中,点
中,点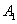 ,
, ,
,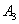 ,…,
,…, 在
在 轴的正半轴上,且
轴的正半轴上,且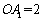 ,
, ,
, ,…,
,…, ,点
,点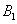 ,
, ,
, ,…,
,…,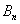 在第一象限的角平分线l上,且
在第一象限的角平分线l上,且 ,
, ,…,
,…, 都与射线l垂直,则
都与射线l垂直,则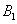 的坐标是_ _____,
的坐标是_ _____,  的坐标是_ _____,
的坐标是_ _____,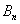 的坐标是_ _____.
的坐标是_ _____.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
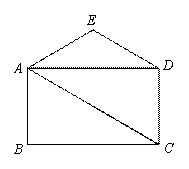
如图,四边形ABCD为矩形,DE∥AC,且DE=AB,过点E作AD的垂线交AC于点F.
(1)依题意补全图,并证明四边形EFCD是菱形;
(2)若AB=3,BC=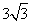 ,求平行线DE与AC间的距离.
,求平行线DE与AC间的距离.
 |
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山西农业大学附属中学八年级上学期期末考试数学试卷(解析版) 题型:解答题
(10分)一个正方形的边长增加3cm,它的面积就增加39cm2,这个正方形的边长是多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本小题6分)已知:如图,DE⊥AC于点E ,BF⊥AC于点F,∠1+∠2=180°,
求证:∠AGF=∠ABC

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )

A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com