
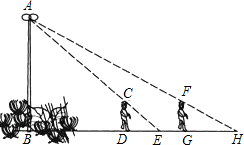
 如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度.
如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度. 分析 根据相似三角形的判定,由CD∥AB得△EAB∽△ECD,利用相似比有$\frac{1.7}{AB}$=$\frac{3}{3+BD}$,同理可得$\frac{1.7}{AB}$=$\frac{4}{BD+5+4}$,然后解关于AB和BD的方程组求出AB即可.
解答 解:∵CD∥AB,
∴△EAB∽△ECD,
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$,即$\frac{1.7}{AB}$=$\frac{3}{3+BD}$①,
∵FG∥AB,
∴△HFG∽△HAB,
∴$\frac{FG}{AB}$=$\frac{HG}{HB}$,即$\frac{1.7}{AB}$=$\frac{4}{BD+5+4}$②,
由①②得$\frac{3}{3+BD}$=$\frac{4}{BD+5+4}$,解得BD=15,
∴$\frac{1.7}{AB}$=$\frac{3}{15+3}$,解得AB=10.2.
答:路灯A离地面的高度为10.2m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
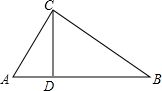 如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}$=$\frac{CD}{BD}$.
如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}$=$\frac{CD}{BD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
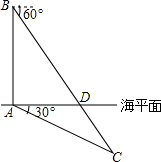 在某联合舰队反潜演习中,军舰A测得潜艇C的俯角为30°,位于军舰A正上方900m的反滑直升机B测得潜艇C的俯角为60°,试求出潜艇C离开海面的下沉深度.
在某联合舰队反潜演习中,军舰A测得潜艇C的俯角为30°,位于军舰A正上方900m的反滑直升机B测得潜艇C的俯角为60°,试求出潜艇C离开海面的下沉深度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com