
【题目】如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
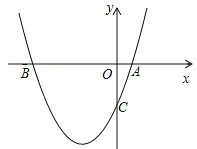
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
【答案】(1)二次函数的解析式为y=x2+2x﹣3。
(2)P(﹣4,5)(2,5)。
【解析】
试题(1)根据曲线上点的坐标与方程的关系,把A(1,0),C(0,﹣3)代入)二次函数y=x2+bx+c中,求出b、c的值,即可得到函数解析式是y=x2+2x﹣3。
∵二次函数y=x2+bx+c过点A(1,0),C(0,﹣3),
∴![]() ,解得
,解得![]() 。
。
∴二次函数的解析式为y=x2+2x﹣3。
(2)求出A、B两点坐标,得到AB的长,再设P(m,n),根据△ABP的面积为10可以计算出n的值,然后再利用二次函数解析式计算出m的值即可得到P点坐标:
∵当y=0时,x2+2x﹣3=0,解得:x1=﹣3,x2=1。
∴A(1,0),B(﹣3,0)。∴AB=4。
设P(m,n),
∵△ABP的面积为10,∴![]() AB|n|=10,解得:n=±5。
AB|n|=10,解得:n=±5。
当n=5时,m2+2m﹣3=5,解得:m=﹣4或2。
∴P(﹣4,5)(2,5)。
当n=﹣5时,m2+2m﹣3=﹣5,方程无解。
∴P(﹣4,5)(2,5)。


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+b与x轴交于点A,与y轴于点B,点C(﹣2,0)在线段OA上,且OC=![]() OA.
OA.
(1)求b的值;
(2)点P是直线y=x+b上一动点,连接PC,PO,求PC+PO的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.
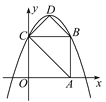
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.

(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com