科目：初中数学 来源：2014-2015学年湖北省七年级5月联考数学试卷（解析版） 题型：解答题
（12分）在平面直角坐标系中，有一点B（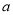
，
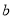）的横纵坐标满足条件：
．
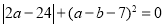（1）（3分）求点B的坐标。
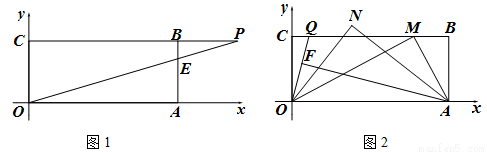
（2）（4分）如图1，过点B作BA⊥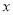
轴于A，BC⊥
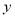轴于C，P为CB延长线上一点，OP交BA于E，若
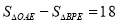，求P、E两点坐标。
（3）（5分）M为（2）中BC上一点，如图2，且OM⊥AM，Q为CM上一动点，F为OQ上一动点，∠FAO=∠COQ，ON、AN分别平分∠QOM与∠FAM，当Q点运动时，∠N变化吗？若不变，求其值；若变化，说明理由。
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省黄冈市罗田县八年级上学期期中联考数学试卷（解析版） 题型：选择题
如图，△ABC中，D是BC中点，DE⊥DF，E、F分别在AB、AC上，则BE+CF（ ）
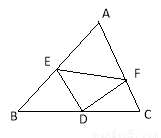
A．大于EF B．等于EF C．小于EF D．与EF的大小无法确定
查看答案和解析>>
科目：初中数学 来源：2014-2015学年重庆市九年级第三次模拟考试数学试卷（解析版） 题型：填空题
有7张正面分别标有数字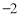
，
，0，1，2，3，4的卡片，除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为m，则使关于x的方程
有实数根，且使不等式组
无解的概率是 ．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年重庆市九年级第三次模拟考试数学试卷（解析版） 题型：选择题
如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为（ ）
A．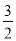
B．2 C．1 D．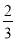
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江绍兴卷）数学（解析版） 题型：解答题
（本题12分）某校规划在一块长AD为18m，宽AB为13m的长方形场地ABCD上，设计分别与AD，AB平行的横向通道和纵向通道，其余部分铺上草皮。
（1）如图1，若设计三条通道，一条横向，两条纵向，且它们的宽度相等，其余六块草坪相同，其中一块草坪两边之比AM:AN=8:9，问通道的宽是多少？
（2）为了建造花坛，要修改（1）中的方案，如图2，将三条通道改为两条通道，纵向的宽度改为横向宽度的2倍，其余四块草坪相同，且每一块草坪均有一边长为8m，这样能在这些草坪建造花坛。如图3，在草坪RPCQ中，已知RE⊥PQ于点E，CF⊥PQ于点F，求花坛RECF的面积。
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江绍兴卷）数学（解析版） 题型：填空题
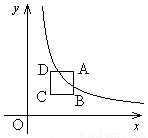
在平面直角坐标系的第一象限内，边长为1的正方形ABCD的边均平行于坐标轴，A点的坐标为（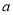
，
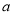）。如图，若曲线
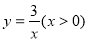与此正方形的边有交点，则
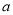的取值范围是 ．
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江衢州卷）数学（解析版） 题型：解答题
小明在课外学习时遇到这样一个问题：
定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．
求函数y=﹣x2+3x﹣2的“旋转函数”．
小明是这样思考的：由函数y=﹣x2+3x﹣2可知，a1=﹣1，b1=3，c1=﹣2，根据a1+a2=0，b1=b2，c1+c2=0，求出a2，b2，c2，就能确定这个函数的“旋转函数”．
请参考小明的方法解决下面问题：
（1）写出函数y=﹣x2+3x﹣2的“旋转函数”；
（2）若函数y=﹣x2+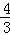
mx﹣2与y=x2﹣2nx+n互为“旋转函数”，求（m+n）2015的值；
（3）已知函数y=﹣
（x+1）（x﹣4）的图象与x轴交于点A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分布是A1，B1，C1，试证明经过点A1，B1，C1的二次函数与函数y=﹣
（x+1）（x﹣4）互为“旋转函数．”
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江嘉兴卷）数学（解析版） 题型：选择题
如图，直线l1// l2// l3，直线AC分别交l1， l2， l3于点A，B，C；直线DF分别交l1， l2， l3于点D，E，F ．AC与DF相较于点H，且AH=2，HB=1，BC=5，则 
的值为（ ）
（A）
（B）2 （C）
（D）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的自变量x取值范围（ ）
B．
C．
D．
