Question

3．已知：直线l₁：y=-x+n过点A（-1，3），双曲线Cy=$\frac{m}{x}$（x＞0）过点B（1，2），动直线l₂：y=kx-2k+2（常数k＜0）恒过定点F．
（1）求直线l₁，双曲线C的解析式，定点F的坐标；
（2）在双曲线C上取一点P（x，y），过P作x轴的平行线交直线l₁于M，连接PF．求证：PF=PM．
（3）若动直线l₂与双曲线C交于P₁，P₂两点，分别过P₁，P₂两点作直线l₁的垂线，垂足分别为M₁，M₂．
求$\frac{{P}_{1}{P}_{2}}{{P}_{1}{M}_{1}+{P}_{2}{M}_{2}}$的值．

Answer 1

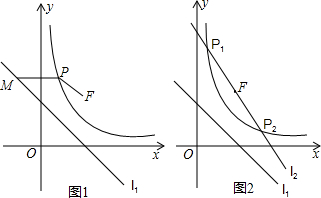
分析 （1）由直线l₁：y=-x+n过点A（-1，3），直接利用待定系数法，即可求得直线l₁，由双曲线C：y=$\frac{m}{x}$（x＞0）过点B（1，2），直接利用待定系数法，即可求得双曲线C的解析式，又由动直线l₂：y=kx-2k+2=（k-2）x+2，即可得定点F的坐标为：（2，2）；
（2）首先在双曲线C上任取一点P（x，y），过P作x轴的平行线交直线l₁于M（x₀，y），连结PF，可得PF=x-x₀，又由M（x₀，y）在直线l₁上，可得-x₀+2=y，继而可得PM=x+$\frac{2}{x}$-2，然后求得PF，即可证得PM=PF；
（3）首先分别过P₁，P₂作x轴的平行线交直线l₁于M₁′，M₂′两点，易得△P₁M₁M₁′和△P₂M₂M₂′都是等腰直角三角形，继而求得P₁M₁=$\frac{\sqrt{2}}{2}$P₁M₁′，P₂M₂=$\frac{\sqrt{2}}{2}$P₂M₂′，然后由（2）可知，P₁M₁′+P₂M₂′=P₁F+P₂F=P₁P₂，即可求得答案．

解答 解：（1）∵直线直线l₁：y=-x+n过点A（-1，3），
∴-（-1）+n=3，
解得：n=2，
∴直线l₁的解析式为y=-x+2；
∵双曲线C：y=$\frac{m}{x}$（x＞0）过点B（1，2），
∴$\frac{m}{1}$=2，
解得：m=2，
∴即双曲线C的解析式为：y=$\frac{2}{x}$，
动直线动直线l₂：y=kx-2k+2=（k-2）x+2，
∴不论k为任何负数时，当x=2时，则y=2，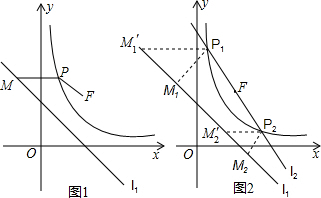
即动直线l₂：y=kx-2k+2恒过定点F（2，2）；

（2）如图1，在双曲线C上任取一点P（x，y），过P作x轴的平行线交直线l₁于M（x₀，y），连结PF．
则PF=x-x₀，
又∵M（x₀，y）在直线l₁上，
∴-x₀+2=y，
∴x₀=2-y=2-$\frac{2}{x}$，
∴PM=x+$\frac{2}{x}$-2，
又∵PF=$\sqrt{（x-2）^{2}+（y-2）^{2}}$=$\sqrt{（x-2）^{2}+（\frac{2}{x}-2）^{2}}$=$\sqrt{{x}^{2}-4x+4+\frac{2}{{x}^{2}}-\frac{8}{x}+4}$=$\sqrt{（{x}^{2}+\frac{4}{{x}^{2}}）-4（x+\frac{2}{x}）+4+4}$=$\sqrt{（x+\frac{2}{x}）^{2}-4（x+\frac{2}{x}）+4}$=$\sqrt{（x+\frac{2}{x}-2）^{2}}$=x+$\frac{2}{x}$-2，
（注：x+$\frac{2}{x}$-2=（$\sqrt{x}$）²+（$\sqrt{\frac{2}{x}}$）²-2$\sqrt{x}$•$\sqrt{\frac{2}{x}}$+2$\sqrt{2}$-2=（$\sqrt{x}$-$\sqrt{\frac{2}{x}}$）²+2$\sqrt{2}$-2≥2$\sqrt{2}$-2＞0）
∴PM=PF；

（3）分别过P₁，P₂作x轴的平行线交直线l₁于M₁′，M₂′两点，
∵直线l₁的解析式为y=-x+2，
∴△P₁M₁M₁′和△P₂M₂M₂′都是等腰直角三角形．
∴P₁M₁=$\frac{\sqrt{2}}{2}$P₁M₁′，P₂M₂=$\frac{\sqrt{2}}{2}$P₂M₂′，
由（2）可知，P₁M₁′+P₂M₂′=P₁F+P₂F=P₁P₂，
∴$\frac{{P}_{1}{P}_{2}}{{P}_{1}{M}_{1}+{P}_{2}{M}_{2}}$=$\frac{{P}_{2}{P}_{2}}{{\frac{\sqrt{2}}{2}P}_{1}{M}_{1}^{′}+{\frac{\sqrt{2}}{2}P}_{2}{M}_{2}^{′}}$=$\frac{{P}_{1}{P}_{2}}{\frac{\sqrt{2}}{2}（{P}_{1}{M}_{1}^{′}+{P}_{2}{M}_{2}^{′}）}$=$\frac{{P}_{1}{P}_{2}}{\frac{\sqrt{2}}{2}（{P}_{1}F+{P}_{2}F）}$=$\frac{{P}_{1}{P}_{2}}{\frac{\sqrt{2}}{2}{P}_{1}{P}_{2}}$=$\sqrt{2}$．

点评 此题属于反比例函数综合题，考查了待定系数求函数解析式的知识、勾股定理以及等腰直角三角形性质．注意准确作出辅助线是解此题的关键．