
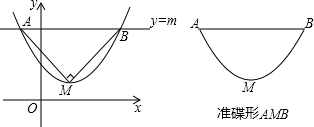
| A. | mn>-9 | B. | -9≤mn≤0 | C. | -4≤mn≤0 | D. | mn≥-9且mn≠0 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.
如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “a是任意实数,则a2≥0”是随机事件 | |
| B. | 某彩票的中奖率为1%,则买100张彩票一定有1张会中奖 | |
| C. | 若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为$\frac{1}{2}$ | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{a}$ | B. | $\frac{a}{{x}^{2}}$ | C. | $\frac{{a}^{2}}{x}$ | D. | $\frac{x}{{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
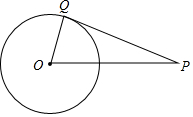 如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切
如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com