
【题目】小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。

科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为1的正方形OA![]() B
B![]() C
C![]() 的顶点A
的顶点A![]() 在X轴的正半轴上,如图将正方形OA
在X轴的正半轴上,如图将正方形OA![]() B
B![]() C
C![]() 绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图像上,
绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图像上,
则a的值为___________.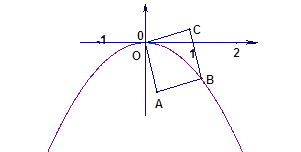
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,∠AOB=30°,点M为射线OB上一点,平面内有一点P使∠PAM=150°且PA=AM.

(1)求证:∠OMA=∠OAP.
(2)如图2,若射线OB上有一点Q使∠POA=∠AQO,求证:OP=AQ.
(3)如图3,在(2)的条件下,过A作AH⊥OB,且OH=![]() AH,已知N点为MQ的中点,且ON=
AH,已知N点为MQ的中点,且ON=![]() ,则OA=____________.
,则OA=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,BC=1,
中,BC=1,![]() .
.

(1)求AB的长度:
(2)过点A作AB的垂线,交AC的垂直平分线于点D ,以AB为一边作等边![]() .
.
①连接CE,求证: BD=CE;
②连接DE交AB于F.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.

(1)三角形的外角等于与它不相邻的两个内角的______,若∠A=45°,∠B=30°,则∠BEC=______;
(2)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(3)试猜想∠BOC与∠A、∠B、∠C之间的关系,并证明你猜想的正确性。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx+n交坐标轴分别于A,B(0,1)两点,交双曲线y=![]() 于点C(2,2),点D在直线AB上,AC=2CD.过点D作DE⊥x轴于点E,交双曲线y=
于点C(2,2),点D在直线AB上,AC=2CD.过点D作DE⊥x轴于点E,交双曲线y=![]() 于点F,连接CF.
于点F,连接CF.
(1)求反比例函数y=![]() 和直线y=mx+n的表达式;
和直线y=mx+n的表达式;
(2)求△CDF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com