
【题目】如图1,∠AOB=30°,点M为射线OB上一点,平面内有一点P使∠PAM=150°且PA=AM.

(1)求证:∠OMA=∠OAP.
(2)如图2,若射线OB上有一点Q使∠POA=∠AQO,求证:OP=AQ.
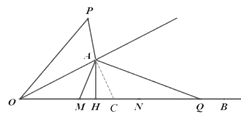
(3)如图3,在(2)的条件下,过A作AH⊥OB,且OH=![]() AH,已知N点为MQ的中点,且ON=
AH,已知N点为MQ的中点,且ON=![]() ,则OA=____________.
,则OA=____________.
【答案】(1)见解析;(2)见解析;(3)2
【解析】
(1)利用三角形的内角和定理可得∠OAM+∠OMA=150°,再由条件∠OAP+∠OAM=150°,即可得出结论;
(2)在OB上取一点M使AM=AN,然后证明△OAP≌QNA即可得出结论;
(3)在OB上取一点C使AM =AC,设AH=x,MH=CH=y,然后用含x、y的式子表示出ON,再利用ON=![]() 建立方程求出x,即可得出答案.
建立方程求出x,即可得出答案.
(1)证明:∵∠AOB=30°,
∴∠OAM+∠OMA=150°,
∵∠PAM=∠OAP+∠OAM=150°,
∴∠OAP=∠OMA;
(2)证明:在OB上取一点M使AM=AN,
∴∠AMN=∠ANM,
∵∠AMO+∠AMN=180°,∠ANM+∠ANQ=180°,
∠AMO=∠ANQ,
∵∠AMO=∠OAP,
∴∠OAP=∠ANQ,
在△OAP和△QNA中
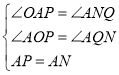
∴△OAP≌QNA(AAS),
∴OP=AQ;
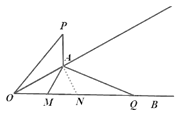
(3)在OB上取一点C使AM =AC,
由(2)知△OAP≌△ACQ,
∴OA=CQ,
设AH=x,则OA=CQ =2x,OH=![]() x.
x.
设MH=CH=y,
∴MQ=MC+CQ=2x+2y,
∵N是MQ中点,
∴MN=x+y,
∵OM=OH-MH=![]() x-y,
x-y,
∴ON=OM+MN=x+y+![]() x-y=1+
x-y=1+![]() ,
,
解得x=1,
∴OA=2x=2.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC=![]() ,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )
,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC与直角三角形BDE中,点B,C,D在同一条直线上,已知AC=AE=CD,∠BAC和∠ACB的角平分线交于点F,连DF,EF,分别交AB、BC于M、N,已知点F到△ABC三边距离为3,则△BMN的周长为____________.
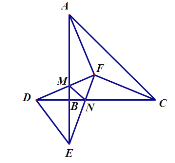
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=5,AD=BC=13,点E为射线AD上的一个动点,若△ABE与△A'BE关于直线BE对称,当△A'BC为直角三角形时,AE的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com