
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.

(1)三角形的外角等于与它不相邻的两个内角的______,若∠A=45°,∠B=30°,则∠BEC=______;
(2)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(3)试猜想∠BOC与∠A、∠B、∠C之间的关系,并证明你猜想的正确性。
【答案】(1)和,75°;(2)30°;(3)∠BOC=∠A+∠B+∠C ,理由见解析
【解析】
(1)直接利用三角形的外角的性质求出;
(2)先利用三角形的外角的性质求出∠BDO=80°,最后用三角形的内角和定理即可得出结论;
(2)利用三角形的外角的性质即可得出结论.
(1) 三角形的外角等于与它不相邻的两个内角的和,
∵∠A=45°,∠B=30°
∴![]() ,
,
(2)∵∠A=50°,∠C=30°
∴![]()
∵∠BOD=70°
∴在△BOD中,∠B=180°- ∠BOD- ∠BDO
=180°-70°-80°
=30°
(3)∠BOC=∠A+∠B+∠C ,理由如下:
∵∠BOC=∠B+∠BDO,∠BDO=∠A+∠C
∴∠BOC=∠A+∠B+∠C


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
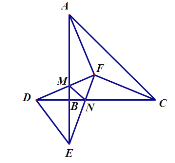
【题目】如图,直角三角形ABC与直角三角形BDE中,点B,C,D在同一条直线上,已知AC=AE=CD,∠BAC和∠ACB的角平分线交于点F,连DF,EF,分别交AB、BC于M、N,已知点F到△ABC三边距离为3,则△BMN的周长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.

(1)求证:△ACE≌△BCF;
(2)若∠BFE=60°,求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=5,AD=BC=13,点E为射线AD上的一个动点,若△ABE与△A'BE关于直线BE对称,当△A'BC为直角三角形时,AE的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )

A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】法国数学家柯西于1813年在拉格朗日、高斯的基础上彻底证明了《费马多边形数定理》,其主要突破在“五边形数”的证明上.如图为前几个“五边形数”的对应图形,请据此推断,第10个“五边形数”应该为( ),第2018个“五边形数”的奇偶性为( )

A. 145;偶数 B. 145;奇数 C. 176;偶数 D. 176;奇数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ ABC中,AB=AC,∠ BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△ EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com