练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知∠BDA=∠CDA，则不一定能使△ABD≌△ACD的条件是（　　）

    A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD

    【答案】B

    【解析】试题解析：A.BD=DC,∠BDA=∠CDA,AD=AD,符合全等三角形的判定定理SAS,能推出△ABD≌△ACD，故本选项错误；

    B.AB=AC,∠BDA=∠CDA,AD=AD,不符合全等三角形的判定定理,不能推出△ABD≌△ACD，故本选项正确；

    C.∠B=∠C,∠BDA=∠CDA,AD=AD,符合全等三角形的判定定理AAS,能推出△ABD≌△ACD，故本选项错误；

    D.∠BDA=∠CDA,AD=AD,∠BAD=∠CAD,符合全等三角形的判定定理ASA,能推出△ABD≌△ACD，故本选项错误；

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系（如图1），y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．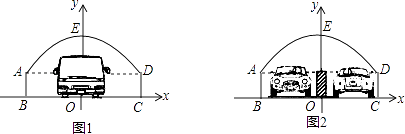

    （1）求抛物线的解析式；
    （2）现有一辆货运卡车，高4.4m，宽2.4m，它能通过该隧道吗？
    （3）如果该隧道内设双向道（如图2），为了安全起见，在隧道正中间设有0.4m的隔离带，则该辆货运卡车还能通过隧道吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：
    ①abc＜0；②b2﹣4ac＞0；③3a+c＜0；④16a+4b+c＞0．
    其中正确结论的个数是（ ）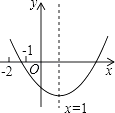

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，所有房间刚好可以住满，根据经验发现，每个房间的定价每增加10元，就会有1个房间空闲，对有游客入住的房间，宾馆需对每个房间支出每天20元的各种费用．设每个房间的定价增加x元，每天的入住量为y个，客房部每天的利润为w元．
    （1）求y与x的函数关系式；
    （2）求w与x的函数关系式，并求客房部每天的最大利润是多少？
    （3）当x为何值时，客房部每天的利润不低于14000元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，Rt△ABC中，∠ABC=90°，BC＜AB＜2BC．在AB边上取一点M，使AM=BC，过点A作AE⊥AB且AE=BM，连接EC，再过点A作AN∥EC，交直线CM、CB于点F、N．

    （1）证明：∠AFM=45°；

    （2）若将题中的条件“BC＜AB＜2BC”改为“AB＞2BC”，其他条件不变，请你在图2的位置上画出图形，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，请猜想∠AFM的度数，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=1与抛物线y=x2﹣2x相交于M，N两点，则M，N两点的横坐标是下列哪个方程的解？（ ）

    A.x2﹣2x+1=0
    B.x2﹣2x﹣1=0
    C.x2﹣2x﹣2=0
    D.x2﹣2x+2=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小鹏和小娟玩一种游戏：小鹏手里有三张扑克牌分别是3、4、5，小娟有两张扑克牌6、7，现二人各自把自己的牌洗匀，小鹏从小娟的牌中任意抽取一张，小娟从小鹏的牌中任意抽取一张，计算两张数字之和，如果和为奇数，则小鹏胜；如果和为偶数则小娟胜．
    （1）用列表或画树状图的方法，列出小鹏和小娟抽得的数字之和所有可能出现的情况；
    （2）请判断该游戏对双方是否公平？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，对角线AC，BD相交于点O，过点O与AD上的一点E作直线OE，交BA的延长线于点F．若AD=4，DC=3，AF=2，则AE的长是（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与x、y轴交于点A（1，0），B（0，﹣1）与反比例函数y= 在第一象限内的图象交于点C，点C的纵坐标为1．

    （1）求一次函数的解析式；
    （2）求点C的坐标及反比例函数的解析式．

    查看答案和解析>>

    同步练习册答案