
【题目】如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 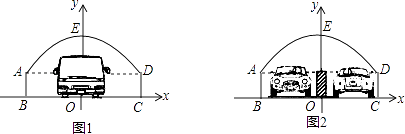
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
【答案】
(1)解:∵OE为线段BC的中垂线,
∴OC= ![]() BC.
BC.
∵四边形ABCD是矩形,
∴AD=BC=8m,AB=CD=2m,
∴OC=4.
∴D(4,2,).E(0,6).
设抛物线的解析式为y=ax2+c,由题意,得
![]() ,
,
解得: 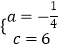 ,
,
∴y=﹣ ![]() x2+6
x2+6
(2)解:由题意,得
当y=4.4时,4.4=﹣ ![]() x2+6,
x2+6,
解得:x=± ![]() ,
,
∴宽度为: ![]() >2.4,
>2.4,
∴它能通过该隧道
(3)解:由题意,得
![]() (
( ![]() ﹣0.4)=
﹣0.4)= ![]() ﹣0.2>2.4,
﹣0.2>2.4,
∴该辆货运卡车还能通过隧道
【解析】(1)抛物线的解析式为y=ax2+c,根据E点及D点的坐标由待定系数法就可以求出结论;(2)当y=2.4时代入(1)的解析式求出x的值就求出结论;(3)将(2)求出的宽度﹣0.4m后除以2的值与2.4比较就可以求出结论.


科目:初中数学 来源: 题型:
【题目】在计算![]() 的过程中,三位同学给出了不同的方法:
的过程中,三位同学给出了不同的方法:
甲同学的解法:原式=![]() ;
;
乙同学的解法:原式=![]() =1;
=1;
丙同学的解法:原式=(x+3)(x﹣2)+2﹣x=x2+x﹣6+2﹣x=x2﹣4.
(1)请你判断一下, 同学的解法从第一步开始就是错误的, 同学的解法是完全正确的.
(2)乙同学说:“我发现无论x取何值,计算的结果都是1”.请你评价一下乙同学的话是否合理,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
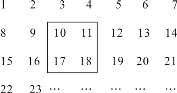
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() ,AD平分∠CAB,交CB于点D,过点D作
,AD平分∠CAB,交CB于点D,过点D作![]() 于点E.若
于点E.若![]() ,CD=5,.
,CD=5,.
(1)求BD的长
(2)AE与BE相等吗?说明理由。
(3)求△ABC的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用棋子摆成的“上”字.
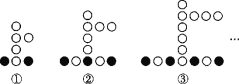
(1)依照此规律,第4个图形需要黑子、白子各多少枚?
(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子、白子各多少枚?
(3)请探究第几个“上”字图形白子总数比黑子总数多15枚.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列关系错误的是( )

A. ∠AOC=∠AOB+∠BOC
B. ∠AOC=∠AOD-∠COD
C. ∠AOC=∠AOB+∠BOD-∠BOC
D. ∠AOC=∠AOD-∠BOD+∠BOC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开学,两摞规格相同准备发放的数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题:
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示);
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )

A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com