
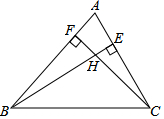
 在△ABC中,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,
在△ABC中,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,分析 (1)先根据三角形的内角和定理求出∠A的度数,再由BE⊥AC可知∠AEB=90°,由直角三角形的性质即可求出∠ABE的度数,然后依据三角形的外角的性质可得到∠BHC的度数;
(2)依据面积法可得到AB•FC=AC•BE,从而可求得问题的答案.
解答 解:(1)∵△ABC中,∠ABC=62°,∠ACB=50°,
∴∠A=180°-∠ABC-∠ACB=180°-62°-50°=68°,
∵BE⊥AC,
∴∠AEB=90°,
∴∠ABE=90°-∠A=90°-68°=22°;
∵CF⊥AB,
∴∠BFC=90°,
∴∠BHC=∠ABF+∠BFH=90°+22°=112°.
(2)∵S△ABC=$\frac{1}{2}$AB•FC=$\frac{1}{2}$AC•BE,
∴AB•FC=AC•BE,即8BE=40,解得:BE=5.
点评 本题主要考查的是三角形内角和定理的应用和三角形的面积公式,面积法的应用是解题的关键.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
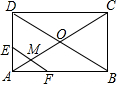 如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )| A. | 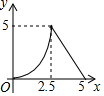 | B. | 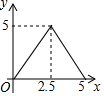 | C. | 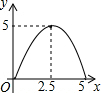 | D. | 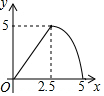 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
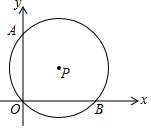 如图,⊙P与两条坐标轴分别交于点A、O、B,若点A、B的坐标分别为(0,6)、(8,0),则圆心P的坐标为( )
如图,⊙P与两条坐标轴分别交于点A、O、B,若点A、B的坐标分别为(0,6)、(8,0),则圆心P的坐标为( )| A. | (4,3) | B. | (3,4) | C. | (3,3) | D. | (4,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同角的余角相等 | |
| B. | 等腰三角形的两个底角相等 | |
| C. | 两直线平行,内错角相等 | |
| D. | 线段中垂线上的点到线段两端的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
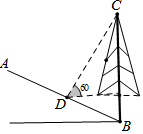 如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com