
【题目】已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
【答案】(1)点P的坐标为(![]() ,3).
,3).
(2)抛物线的解析式为y=﹣x2+6
(3)点A、B、C、D围成的多边形的面积为4+2![]() 或6
或6![]() .
.
【解析】
试题(1)由切线的性质可得∠MPO=90°,由勾股定理可求出PO,由三角形PMO的面积利用面积法可求出PK,然后再运用勾股定理可求出OK,就可得到点P的坐标.
(2)可设顶点为(0,6)的抛物线的解析式为y=ax2+6,然后将点P的坐标代入就可求出抛物线的解析式.
(3)直线y=m与⊙M相切有两种可能,只需对这两种情况分别讨论就可求出对应多边形的面积.
试题解析:(1)如图1,

∵⊙M与OP相切于点P,
∴MP⊥OP,即∠MPO=90°.
∵点M(0,4)即OM=4,MP=2,
∴OP=2![]() .
.
∵⊙M与OP相切于点P,⊙M与OQ相切于点Q,
∴OQ=OP,∠POK=∠QOK.
∴OK⊥PQ,QK=PK.
∴PK=![]() .
.
∴OK=![]() =3.
=3.
∴点P的坐标为(![]() ,3).
,3).
(2)如图2,

设顶点为(0,6)的抛物线的解析式为y=ax2+6,
∵点P(![]() ,3)在抛物线y=ax2+6上,
,3)在抛物线y=ax2+6上,
∴3a+6=3.
解得:a=﹣1.
则该抛物线的解析式为y=﹣x2+6.
(3)当直线y=m与⊙M相切时,
则有![]() =2.
=2.
解得;m1=2,m2=6.
①m=2时,如图3,

则有OH=2.
当y=2时,解方程﹣x2+6=2得:x=±2,
则点C(2,2),D(﹣2,2),CD=4.
同理可得:AB=2![]() .
.
则S梯形ABCD=![]() (DC+AB)OH=
(DC+AB)OH=![]() ×(4+2
×(4+2![]() )×2=4+2
)×2=4+2![]() .
.
②m=6时,如图4,
此时点C、点D与点N重合.

S△ABC=![]() ABOC=
ABOC=![]() ×2
×2×6=6
![]() .
.
综上所述:点A、B、C、D围成的多边形的面积为4+2![]() 或6
或6![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由物理学知识知道,在力F的作用下,物体会在力F的方向上发生位移s,力所做的功W=Fs.当W为定值时,F与s之间的函数关系图象如图所示.
(1)力F所做的功是多少?
(2)试确定F、s之间的函数解析式;
(3)当F=4N时,s是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数值随自变量增大而增大 B. 函数图像与![]() 轴正方向成45°角
轴正方向成45°角
C. 函数图像不经过第四象限 D. 函数图像与![]() 轴交点坐标是(0,6)
轴交点坐标是(0,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°, BC∥x轴,抛物线y=ax2-2ax+3经过△ABC的三个顶点,并且与x轴交于点D、E,点A为抛物线的顶点.

(1)求抛物线的解析式;
(2)连接CD,在抛物线的对称轴上是否存在一点P使△PCD为直角三角形,若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(kg)与上市时间x(天)的函数关系如图1,樱桃价格z(元/kg)与上市时间x(天)的函数关系式如图2.

(1)求小明家樱桃的日销售量y与上市时间x的函数解析式.
(2)求当5≤x≤20时,樱桃的价格z与上市时间x的函数解析式.
(3)求哪一天的销售金额达到最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE⊥AC于点E,BC的垂直平分线分别交AB、BE于点D、G,垂足为H,CD⊥AB,CD交BE于点F

(1)求证:△BDF≌△CDA,并写出BF与AC的数量关系.
(2)若DF=DG,求证:①BE平分∠ABC; ②CE=![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解全校1600名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,8),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
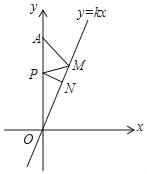
A. 4 B. 4![]() C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com