
【题目】如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.求证:BD平分∠EBC.


【答案】证明见解析.
【解析】试题分析:(1)先根据对顶角相等得出∠2=∠ABE,再由∠1=∠2可知∠1=∠ABE,根据平行线的判定定理即可得出:AB∥CD,然后根据平行线的性质可知∠AED+∠BAE=180°,∠BEF=∠EBC,根据∠BAE=∠BDE可得∠AED+∠BDE=180°,故AE∥BD,所以∠AEB=∠DBE,再根据EA平分∠BEF可得出结论.
试题解析:证明:∵∠1=∠2,∠2=∠ABE,
∴∠1=∠ABE,
∴AB∥DF;
∴∠AEF=∠BAE, ∠BEF=∠EBC,
∵∠BAE=∠BDE
∴∠AEF=∠BDE
∴AE∥BD;
∴∠AEB=∠DBE
∵EA平分∠BEF
∴∠AEB=![]() ∠BEF
∠BEF
∵∠BEF=∠EBC, ∠AEB=∠DBE,
∴∠DBE=![]() ∠EBC
∠EBC
∴BD平分∠EBC


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查最适合用查阅资料的方法收集数据的是( )
A. 班级推选班长 B. 本校学生的到时间
C. 2014世界杯中,谁的进球最多 D. 本班同学最喜爱的明星
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沈阳地铁一号线的开通运行给沈阳市民的出行方式带来了一些变化.小王和小林准备利用课余时间,以问卷的方式对沈阳市民的出行方式进行调查.如图是沈阳地铁一号线图(部分),小王和小林分别从太原街站(用A表示)、南市场站(用B表示)、青年大街站(用C表示)这三站中,随机选取一站作为调查的站点.
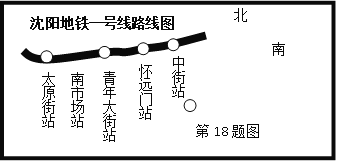
⑴在这三站中,小王选取问卷调查的站点是太原街站的概率是多少?(请直接写出结果)
⑵请你用列表法或画树状图(树形图)法,求小王选取问卷调查的站点与小林选取问卷调查的站点相邻的概率.(各站点用相应的英文字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列信息;据报道,全世界受到威胁的动物种类数如下表所示.请你按照下面要求回答问题:
全世界受到威胁的动物种类数 | ||||
动物分类 | 哺乳类 | 鸟类 | 爬行类 | 两栖类 |
受到威胁的种类数(种) | 约1100 | 约1100 | 约300 | 约100 |
(1)制作适当的统计图表示表中的数据,你选择的统计图是____________________;
(2)通过学习本题,请你写一句20字左右的感想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察、思考、解答: ( ![]() ﹣1)2=(
﹣1)2=( ![]() )2﹣2×1×
)2﹣2×1× ![]() +12=2﹣2
+12=2﹣2 ![]() +1=3﹣2
+1=3﹣2 ![]()
反之3﹣2 ![]() =2﹣2
=2﹣2 ![]() +1=(
+1=( ![]() ﹣1)2
﹣1)2
∴3﹣2 ![]() =(
=( ![]() ﹣1)2
﹣1)2
∴ ![]() =
= ![]() ﹣1
﹣1
(1)仿上例,化简: ![]() ;
;
(2)若 ![]() ,则m、n与a、b的关系是什么?并说明理由;
,则m、n与a、b的关系是什么?并说明理由;
(3)已知x= ![]() ,求(
,求( ![]() )
) ![]() 的值(结果保留根号)
的值(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
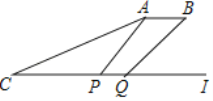
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com