
(12分)如图,AB=AC,AE=AF,∠BAC=∠EAF=90°,BE、CF交于M,连AM.
⑴求证:BE=CF;⑵求证:BE⊥CF;⑶求∠AMC的度数.

(1)见解析;(2)见解析;(3)135°
【解析】
试题分析:⑴证△BEA≌△CFA.⑵∠ABE=∠ACF,∴∠CMB=∠CAB=90°.
⑶作AG⊥BE于G,AH⊥CF于H,证△AGB≌△AHC,AG=AH,∠AMG=45°,可得∠AMC=135°
试题解析:(1)∵∠BAC=∠EAF=90°
∴∠BAE=∠CAF
∵ AE=AF,AB=AC,
∴三角形BAE 全等于 三角形CAF,
∴ BE=CF
(2)∵∠AEB=∠AFC
设CF与AE相交于点H 则∠MHE = ∠AHF
∵三角形EMH与三角形 HAF的内角和都为180°
∴ ∠EMF = ∠EAF
即BE⊥CF
(3)∵∠ABE=∠ACF
∴ A,B,C,M四点共圆
∴ ∠AMC+∠ABC=180°
∵AB=AC,∠BAC=90°,∠ABC=45°
∴ ∠AMC=180°--∠ABC=135°
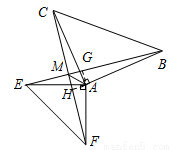
也可以作AG⊥BE于G,AH⊥CF于H,证△AGB≌△AHC,AG=AH,∠AMG=45°,可得∠AMC=135.
考点:


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年湖北省宜城市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分7分)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=xm.

(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省通山县九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)如图,在平面直角坐标系中,已知点B的坐标是(-1,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.

(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,写出点P的坐标(不要求写解题过程).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省八年级上学期期中数学试卷(解析版) 题型:解答题
(10分)如图,△ABC中,∠C=2∠A,BD平分∠ABC交AC于D,求证:AB=CD+BC.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省七年级上学期期中考试数学试卷(解析版) 题型:选择题
根据国家统计局的数据,我国今年1-9月份国内生产总值419908亿,第三季度GDP增长7.3%,创下5年半以来的新低,前三季度同比增长7.4%.则近似数7.4%精确到( )
A.十分位 B.百分位 C.千分位 D.万分位
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省七年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律.则第(n)个图形中面积为1的正方形的个数为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省黄石市九年级10月月考数学试卷(解析版) 题型:解答题
二次函数 的图象如图所示,根据图象:
的图象如图所示,根据图象:

(1)求其解析式(3分)
(2)观察图像写出 >0时
>0时 的取值范围(3分)
的取值范围(3分)
(3)是否存在某直线经过A(1,0)并与该抛物线只有一个公共点?若存在,求出该直线的解析式,若不存在,请说明理由(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com