练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

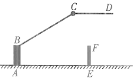
    【题目】一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD=150°，求∠ABC的度数.

    【答案】120°.

    【解析】

    首先过点B作BF∥CD，由CD∥AE，可得CD∥BF∥AE，继而证得∠1＋∠BCD＝180°，∠2＋∠BAE＝180°，又由BA垂直于地面AE于A，∠BCD＝150°，求得答案．

    如图，过点B作 BG∥AE.

    ∵CD∥AE，

    ∴BG∥CD，

    ∴∠GBC＋∠BCD ＝180°.又∠BCD＝ 150°，

    ∴∠GBC＝180°－∠BCD＝180o －150°＝30°.

    ∵BA⊥AE，∴∠BAE ＝ 90°.

    ∵BG∥AE，

    ∴∠GBA＋∠BAE ＝180°，

    ∴∠GBA＝180°－∠BAE ＝90°.

    ∴∠ABC＝∠GBA＋∠GBC＝90°＋30°＝120°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知E、F分别是ABCD的边BC、AD上的点，且BE=DF．

    （1）求证：四边形AECF是平行四边形；

    （2）若∠BAC=90°，AC平分∠EAF，且BC=8cm，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D是以点A为圆心4为半径的圆上一点，连接BD，点M为BD中点，线段CM长度的最大值为 ．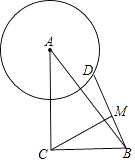

    查看答案和解析>>

    科目：初中数学 来源： 题型：

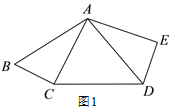
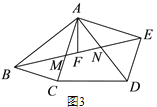
    【题目】如图 1，在五边形 ABCDE 中，∠E=90°，BC=DE.连接 AC，AD， 且 AB=AD，AC⊥BC.

    （1）求证：AC=AE；

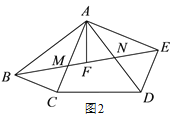
    （2）如图 2，若∠ABC=∠CAD，AF 为 BE 边上的中线，求证：AF⊥CD；

    （3）如图 3，在（2）的条件下，AE=6，DE=4，则五边形 ABCDE 的面积为_____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

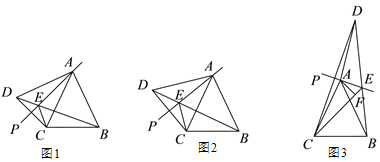
    【题目】在△ABC 中，AB=AC，∠CAB=50°.在△ABC 的外侧作直线 AP，作 点 C 关于直线 AP 的对称点 D，连接 BD，CD，AD，其中 BD 交直线 AP 于点 E．

    （1）如图 1，与 AD 相等的线段是_____；

    （2）如图 2，若∠PAC=20°，求∠BDC 的度数；

    （3）如图 3，当 65°<∠PAC<130°时，作 AF⊥CE 于点 F，若 EF=1，BE=5，求 DE 的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C在以AB为直径的半圆上，AB=4 ，AC=4，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE，DF交EC的延长线于点F，当点D从点A运动到点B时，线段EF扫过的面积是 ．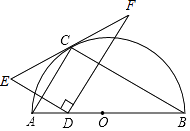

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】快走是大众常用的健身方式，手机中的“乐动力”可以计算行走的步数与消耗的相应能量，对比数据发现小明步行1200步与小红步行9000步消耗的能量相同，若每消耗1千卡能量小明行走的步数比小红多2步，求小红每消耗1千卡能量可以行走多少步？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，添加以下条件，不能判定的是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'=1，则A'D等于（　　）

    A. 2 B. 3 C. D.

    查看答案和解析>>

    同步练习册答案