
【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 . 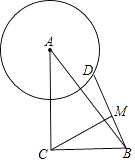
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作ABDE,连接AD、EC. 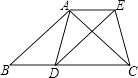
(1)试说明:△ADC≌△ECD;
(2)若BD=CD,试说明:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红学习了用图形面积研究整式乘法的方法后,分别进行了如下数学探究:把一根铁丝截成两段,
探究1:小明截成了两根长度不同的铁丝,并用两根不同长度的铁丝分别围成两个正方形,已知两正方形的边长和为20cm,它们的面积的差为40cm2,则这两个正方形的边长差为 .
探究2:小红截成了两根长度相同的铁丝,并用两根同样长的铁丝分别围成一个长方形与一个正方形,若长方形的长为xm,宽为ym,
(1)用含x、y的代数式表示正方形的边长为 ;
(2)设长方形的长大于宽,比较正方形与长方形面积哪个大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DAB下列条件中不能使△ABC≌△ABD的是( )

A. ∠C=∠D B. ∠ABC=∠ABD C. AC=AD D. BC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,﹣2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).请用列表或树状图的方法(只选其中一种)求出两个数字之积为负数的概率. 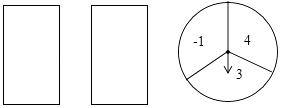
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com