
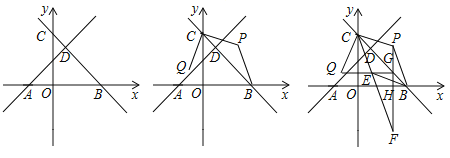
����Ŀ����֪����ͼ1����ƽ��ֱ������ϵ�У���A��B��E�ֱ���x���y���ϵ������. BD�ǡ�ABE��ƽ���ߣ�BD�ķ����ӳ������OAB��ƽ���߽��ڵ�C.
̽���� ��1�����C�Ķ���.
���֣� ��2������A����B�ֱ���x���y������������ƶ�ʱ����C�Ĵ�С�Ƿ����仯�������䣬��ֱ��д�����ۣ��������仯���������C�ı仯��Χ.
Ӧ�ã���3����ͼ2�������ABCDE�У���A����B����E��310����CFƽ�֡�DCB��CF�ķ����ӳ������EDC��ǵ�ƽ�����ཻ�ڵ�P�����P�Ķ�����

���𰸡���1����C=45������2������.��C=![]() ��AOB =45���� (3) 25��.
��AOB =45���� (3) 25��.
��������
��1����ȷ����ABE���OAB�Ĺ�ϵ����ABE=��OAB+90�����ٸ��ݽ�ƽ���ߺ������ε������á�ACB�Ķ�����
��2�����DBC=x����BAC=y���ٸ���BCƽ�֡�DBO��ACƽ�֡�BAO��֪��CBO=��DBC=x����OAC=��BAC=y�����ɡ�DBO����AOB����ǣ���DBC����ABC����ǿɵó�����x��y����C�ķ����飬�����C��ֵ���ɣ�
��3���ӳ�ED��BC�ཻ�ڵ�G�������G�Ķ���������������ǵ����ʿɵý���.
��1���ߡ�ABE=��OAB+��AOB����AOB =90����
���ABE=��OAB+90����
��BD�ǡ�ABE��ƽ���ߣ�ACƽ�֡�OAB��
���ABE=2��ABD����OAB=2��BAC��
��2��ABD=2��BAC+90����
���ABD=��BAC+45����
�֡ߡ�ABD= ��BAC +��C��
���C=45����
��2������.��C=![]() ��AOB =45��.
��AOB =45��.
�������£�
���DBA=x����BAC=y��
��BDƽ�֡�EBA��ACƽ�֡�BAO��
���EBD=��DBA=x����OAC=��BAC=y��
�ߡ�EBA����AOB����ǣ���DBA����ABC����ǣ�
��![]() ��
��
���C=45����
(3) �ӳ�ED��BC�ཻ�ڵ�G.

���ı���ABGE�У�
�ߡ�G��360����(��A����B����E)��50����
���P����FCD����CDP��![]() (��DCB����CDG)
(��DCB����CDG)
��![]() ��G��
��G��![]() ��50����25��.
��50����25��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ͳ��ȥ��1��8��������У�����ȫ��ͬѧ�Ŀ����Ķ���������λ����������������ͼ����ͳ��ͼ������˵����ȷ���ǣ� ��

A.������47B.������42
C.��λ����58D.ÿ���Ķ���������40����4����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣮ֱ��
Ϊ����ԭ�㣮ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() �Ḻ�����ڵ�
�Ḻ�����ڵ�![]() ���ҵ�
���ҵ�![]() ����Ϊ
����Ϊ![]() ��
��
��1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() Ϊֱ��
Ϊֱ��![]() �Ҳ��һ������һ�㣬����
�Ҳ��һ������һ�㣬����![]() ��
��![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת90�����õ��߶�
˳ʱ����ת90�����õ��߶�![]() ����
����![]() ���ڵ�
���ڵ�![]() �������
�������![]() ������Ϊ
������Ϊ![]() �����
�����![]() �����꣨�ú�
�����꣨�ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��3���ڣ�2���������£�����![]() ��
��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬����
�ӳ�����һ�㣬����![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() ��
��![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CD��AB��BE��AC������ֱ�ΪD��E��BE��CD�ཻ�ڵ�O�����AB��AC����ôͼ��ȫ�ȵ�ֱ�������εĶ����ǣ�������

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��AB�ϣ���E��AC�ϣ�AB=AC����B=��C��
��1����֤��BD=CE��
��2����BE��CD���ڵ�F����֤����BDF�ա�CEF��
��3���ڣ�2��������������AF����֤��AFƽ�֡�BAC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�Ƿ���������y= ![]() ��x��0���ϵ�һ�����㣬����OA������O��OB��OA������ʹOB=2OA������AB������A�ڷ��Ⱥ���ͼ�����ƶ�ʱ����BҲ��ijһ����������ͼ��y=
��x��0���ϵ�һ�����㣬����OA������O��OB��OA������ʹOB=2OA������AB������A�ڷ��Ⱥ���ͼ�����ƶ�ʱ����BҲ��ijһ����������ͼ��y= ![]() ���ƶ���k��ֵΪ�� ��
���ƶ���k��ֵΪ�� ��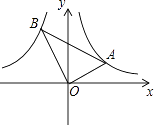
A.2
B.��2
C.4
D.��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��0��������B��b��������������b���㣨a��2��![]() +
+![]() =0����ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��
=0����ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��

��1�����C��D�����꼰�ı���ABDC�������
��2����y�����Ƿ����һ��M������MC��MD��ʹS��MCD=2S�ı���ABDC������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����P��ֱ��BD�ϵ�һ�����㣬����PA��PO������P��ֱ��BD���ƶ�ʱ������B��D�غϣ�ֱ��д����BAP����DOP����APO֮������ ��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�Բ![]() ��
��![]() ��
��![]() �����һ��ƽ�������ߣ���
�����һ��ƽ�������ߣ���![]() ��ԭ��
��ԭ��![]() ���������������������˶����ٶ�Ϊÿ��
���������������������˶����ٶ�Ϊÿ��![]() ����λ���ȣ����2019��ʱ����
����λ���ȣ����2019��ʱ����![]() ��������____��
��������____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����б�µĶ�����һ����AB��B��CD���е㣬CD��ˮƽ�ģ�������������£���ӰDE���������ϣ���֪����������CD=12 m����Ӱ��DE=18 m��С����С�������߶���1.6m��ͬһʱ�̣�С��վ�ڵ�E����Ӱ���������ϣ�С��վ��ƽ���ϣ�Ӱ��Ҳ��ƽ���ϣ����˵�Ӱ���ֱ�Ϊ2m��1m����ô����ABΪ��������

A. 24m B. 22m C. 20m D. 18m
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com