
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是( )

A.1B.2C.3D.4
【答案】C
【解析】
共有3对,分别为△ADC≌△AEB,△BOD≌△COE.Rt△ADO≌Rt△AEO;做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找即可.
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEE=90°,
在△ADC和△AEB中,
∵∠ADC=∠AEB,∠DAC=∠EAB,AC=AB,
∴△ADC≌△AEB(AAS);
∴AD=AE,∠C=∠B,
∵AB=AC,
∴BD=CE,
在△BOD和△COE中,
∵∠B=∠C,∠BOD=∠COE,BD=CE,
∴△BOD≌△COE(AAS);
∴OB=OC,OD=OE,
在Rt△ADO和Rt△AEO中,
∵OA=OA,OD=OE,
∴Rt△ADO≌Rt△AEO(HL);
∴共有3对全等三角形,
故选:C.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式.
(2)D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围.
②当m为何值时,S有最大值,并求这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有 . 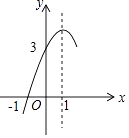
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() 平分
平分![]() ,连结
,连结![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求证:![]() .
.
(3)若![]() ,判定四边形
,判定四边形![]() 是否为菱形,并说明理由.
是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
(Ⅲ)当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,点A,B,E分别是x轴和y轴上的任意点. BD是∠ABE的平分线,BD的反向延长线与∠OAB的平分线交于点C.
探究: (1)求∠C的度数.
发现: (2)当点A,点B分别在x轴和y轴的正半轴上移动时,∠C的大小是否发生变化?若不变,请直接写出结论;若发生变化,请求出∠C的变化范围.
应用:(3)如图2在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC外角的平分线相交于点P,求∠P的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有足够多的长方形和正方形卡片,如下图:

(1)如果选取1号、2号、3号卡片分别为l张、1张、2张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形(所画图形大小和原图保持一致),并用等式表示拼图前后面积之间的关系:
(2)小明用类似方法解释分解因式a2+5ab+4b2,请画图说明小明的方法(所画图形大小和原图保持一致),并写出分解因式的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com