
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式.
(2)D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围.
②当m为何值时,S有最大值,并求这个最大值.
【答案】
(1)解:∵抛物线与x轴交于A(﹣1,0)、B(3,0)两点,
∴设抛物线的解析式为y=a(x+1)(x﹣3),
又∵点C(0,3)在抛物线图象上,
∴3=a×(0+1)×(0﹣3),解得:a=﹣1.
∴抛物线解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3.
故答案为:y=﹣x2+2x+3.
(2)解:①设直线BC的函数解析式为y=kx+b.
∵直线BC过点B(3,0),C(0,3),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴y=﹣x+3.
设D(m,﹣m2+2m+3),E(m,﹣m+3),
∴DE=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m.
∴S= ![]() OBDE=
OBDE= ![]() (﹣m2+3m)=﹣
(﹣m2+3m)=﹣ ![]() m2+
m2+ ![]() m,(0<m<3)
m,(0<m<3)
②S=﹣ ![]() m2+
m2+ ![]() m=﹣
m=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当m= ![]() 时,S有最大值,最大值S=
时,S有最大值,最大值S= ![]()
【解析】(1)因为抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3),用待定系数法求出抛物线的解析式;(2)因为直线BC过点B(3,0),C(0,3),用待定系数法求出直线的解析式,根据△BCD的面积为S,求出s与m的关系,得到m的值,求出S的最大值.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )
A.115°
B.125°
C.120°
D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,点P在AB、CD外部,若∠B=60°,∠D=30°,则∠BPD= °;
(2)如图2,AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)在图2中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图3,若∠BPD=86°,∠BMD=40°,求∠B+∠D的度数.



图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )

A.极差是47B.众数是42
C.中位数是58D.每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用若干块图①所示的长方形和正方形硬纸片可以拼出一些新的长方形,并用不同的方法计算它的面积,从而得到相应的等式.计算图②的面积可以得到等式![]() .
.
①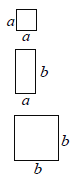 ②
②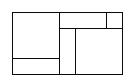
(1)计算图③的面积,可以得到等式__________;
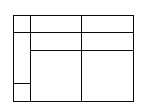 ③
③
(2)在虚线框中用图①所示的长方形和正方形硬纸片若干块(每种至少用一次),拼成一个长方形,使拼出的长方形面积为![]() ,并把二次三项式
,并把二次三项式![]() 分解因式.
分解因式.![]() _______________________;
_______________________;
(3)如图④,大正方形的边长为![]() ,小正方形的边长为
,小正方形的边长为![]() ,若用
,若用![]() 、
、![]() 表示四个长方形的长和宽(
表示四个长方形的长和宽(![]() ),观察图形,指出以下关系式正确的有__________个.
),观察图形,指出以下关系式正确的有__________个.
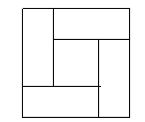

(a)![]() (b)
(b)![]()
(c)![]() (d)
(d)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是( )

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com