
【题目】利用若干块图①所示的长方形和正方形硬纸片可以拼出一些新的长方形,并用不同的方法计算它的面积,从而得到相应的等式.计算图②的面积可以得到等式![]() .
.
①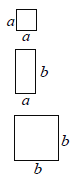 ②
②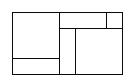
(1)计算图③的面积,可以得到等式__________;
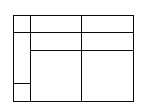 ③
③
(2)在虚线框中用图①所示的长方形和正方形硬纸片若干块(每种至少用一次),拼成一个长方形,使拼出的长方形面积为![]() ,并把二次三项式
,并把二次三项式![]() 分解因式.
分解因式.![]() _______________________;
_______________________;
(3)如图④,大正方形的边长为![]() ,小正方形的边长为
,小正方形的边长为![]() ,若用
,若用![]() 、
、![]() 表示四个长方形的长和宽(
表示四个长方形的长和宽(![]() ),观察图形,指出以下关系式正确的有__________个.
),观察图形,指出以下关系式正确的有__________个.
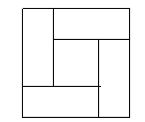

(a)![]() (b)
(b)![]()
(c)![]() (d)
(d)![]()
【答案】(1)(2a+b)(a+2b)=2a2+5ab+2b2;(2)拼出的长方形见解析,2a2+7ab+3b2=(2a+b)(a+3b);(3)4.
【解析】
(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式;
(2)找规律,根据二次三项式画出图形,拼成一个长方形,使它满足所给的条件,再利用另一种计算面积的方法,可将多项式分解因式;
(3)根据图中每个图形的面积之间的关系即可判断出正确的有几个.
解:(1)图③所表示的等式为:(2a+b)(a+2b)=2a2+5ab+2b2;
(2)拼出的长方形如图,
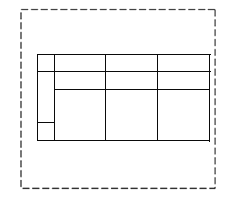
2a2+7ab+3b2=(2a+b)(a+3b);
(3)(a)∵4xy=m2-n2,∴xy=![]() ,正确;
,正确;
(b)正确;
(c)∵x+y=m,x-y=n,
∴x2-y2=(x+y)(x-y)=mn,
∴正确;
(d)x2+y2=(xy)2+2xy=n2+2×![]() =
=![]() ,正确;
,正确;
故正确的有4个,故答案为4.
故答案为(1)(2a+b)(a+2b)=2a2+5ab+2b2;(2)拼出的长方形见解析,2a2+7ab+3b2=(2a+b)(a+3b);(3)4.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式.
(2)D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围.
②当m为何值时,S有最大值,并求这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
⑴小亮行走的总路程是____________cm,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,点B的坐标为(2m,﹣m).
的图象相交于A,B两点,点B的坐标为(2m,﹣m).
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有 . 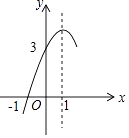
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com