
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
(Ⅲ)当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.
【答案】解:(Ⅰ)∵抛物线过A、C两点,
∴代入抛物线解析式可得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3,
令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,
∵B点在A点右侧,
∴B点坐标为(3,0),
设直线BC解析式为y=kx+s,
把B、C坐标代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC解析式为y=﹣x+3;
(Ⅱ)∵PM⊥x轴,点P的横坐标为m,
∴M(m,﹣m2+2m+3),N(m,﹣m+3),
∵P在线段OB上运动,
∴M点在N点上方,
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,MN有最大值,MN的最大值为
时,MN有最大值,MN的最大值为 ![]() ;
;
(Ⅲ)∵PM⊥x轴,
∴MN∥OC,
当以C、O、M、N为顶点的四边形是平行四边形时,则有OC=MN,
当点P在线段OB上时,则有MN=﹣m2+3m,
∴﹣m2+3m=3,此方程无实数根,
当点P不在线段OB上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,
∴m2﹣3m=3,解得m= ![]() 或m=
或m= ![]() ,
,
综上可知当以C、O、M、N为顶点的四边形是平行四边形时,m的值为 ![]() 或
或 ![]() .
.
【解析】(1)把A、C两点的坐标代入抛物线的解析式中列方程组可求得b,c的值,令y=0,解方程可得B点的坐标,利用待定系数法求直线BC的解析式;(2)根据解析式表示出M、N两点的坐标,其纵坐标的差就是MN的长,配方后求得最值即可;(3)分两种情况:当点P在线段OB上时,则有MN=﹣m2+3m,当点P不在线段OB上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,根据MN=3列方程解出即可。
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,把矩形
中,把矩形![]() 绕点
绕点![]() 旋转,得到矩形
旋转,得到矩形![]() ,且点
,且点![]() 落在
落在![]() 上,连接
上,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,则下列结论:
,则下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ,其中正确的个数是( )
,其中正确的个数是( )
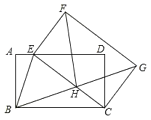
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:

(1)![]() 的顶点都在方格纸的格点上,先将
的顶点都在方格纸的格点上,先将![]() 向右平移2个单位,再向上平移3个单位,得到
向右平移2个单位,再向上平移3个单位,得到![]() ,其中点
,其中点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点,试画出
的对应点,试画出![]() ;
;
(2)连接![]() ,则线段
,则线段![]() 的位置关系为____,线段
的位置关系为____,线段![]() 的数量关系为___;
的数量关系为___;
(3)平移过程中,线段![]() 扫过部分的面积_____.(平方单位)
扫过部分的面积_____.(平方单位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y= ![]() (x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象y=
(x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象y= ![]() 上移动,k的值为( )
上移动,k的值为( )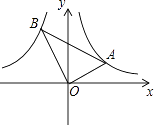
A.2
B.﹣2
C.4
D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店促销,设了有两种摇奖方式:
方式一:如图1,有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上的则获奖:


图1 图2
方式二:如图2,一个均匀的转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字.转动转盘,当转盘停止后,指针指向的数字为3的倍数则获奖.
小明想增加获奖机会,应选择哪种摇奖方式?请通过计算,应用概率相关知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC绕点B顺时针旋转90°得到△A′BC′,请画出△A′BC′.
(2)求BA边旋转到BA′位置时所扫过图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com