
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
【答案】(1)、证明过程见解析;(2)、BD=DE–CE;证明过程见解析;(3)、BD=DE–CE;(4)、当B,C在AE的同侧时,BD=DE–CE;当B,C在AE的异侧时,BD=DE+CE.
【解析】
试题分析:(1)、根据垂直得出∠ADB=∠CEA=90°,结合∠BAC=90°得出∠ABD=∠CAE,从而证明出△ABD和△ACE全等,根据全等得出BD=AE,AD=EC,然后得出答案;(2)、根据第一题同样的方法得出△ABD和△ACE全等,根据全等得出BD=AE,AD=EC,然后得出结论;(3)、根据同样的方法得出结论;(4)、根据前面的结论得出答案.
试题解析:(1)∵BD⊥AE,CE⊥AE ∴∠ADB=∠CEA=90° ∴∠ABD+∠BAD=90° 又∵∠BAC=90°
∴∠EAC+∠BAD=90° ∴∠ABD=∠CAE
在△ABD与△ACE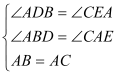 ∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE+CE
∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE+CE
(2)、∵BD⊥AE,CE⊥AE ∴∠ADB=∠CEA=90° ∴∠ABD+∠BAD=90°
又∵∠BAC=90°∴∠EAC+∠BAD=90° ∴∠ABD=∠CAE
在△ABD与△ACE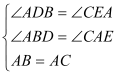 ∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE–CE
∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE–CE
(3)、BD=DE–CE
(4)、归纳:由(1)(2)(3)可知:当B,C在AE的同侧时,BD = DE –CE;当B,C在AE的异侧时,∴BD=DE+CE


科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件![]() 型服装计酬16元,加工1件
型服装计酬16元,加工1件![]() 型服装计酬12元.在工作中发现一名熟练工加工1件
型服装计酬12元.在工作中发现一名熟练工加工1件![]() 型服装和2件
型服装和2件![]() 型服装需4小时,加工3件
型服装需4小时,加工3件![]() 型服装和1件
型服装和1件![]() 型服装需7小时.(工人月工资=底薪+计件工资)
型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件![]() 型服装和1件
型服装和1件![]() 型服装各需要多少小时?
型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工![]() ,
,![]() 两种型号的服装,且加工
两种型号的服装,且加工![]() 型服装数量不少于
型服装数量不少于![]() 型服装的一半”.设一名熟练工人每月加工
型服装的一半”.设一名熟练工人每月加工![]() 型服装
型服装![]() 件,工资总额为
件,工资总额为![]() 元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在□ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,
速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,
点Q也停止移动,如图②.设移动时间为t (s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
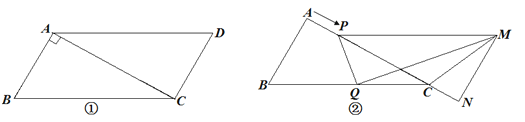
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使![]() ?若存在,求出t的值;若不存在,请说明理由;
?若存在,求出t的值;若不存在,请说明理由;
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家歌德巴赫通过研究下面一系列等式,作出了一个著名的猜想.
4=2+2; 12=5+7;
6=3+3; 14=3+11=7+7;
8=3+5; 16=3+13=5+11;
10=3+7=5+5 18=5+13=7+11;
…
通过这组等式,你发现的规律是 (请用文字语言表达).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形属于因式分解的是( )
A. 4x+x=5xB. (x+2)2=x2+4x+4
C. x2+x+1=x(x+1)+1D. x2﹣3x=x(x﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com