Question

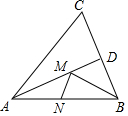
7．如图，在锐角三角形ABC中，AC=6，△ABC的面积为15，∠BAC的平分线交BC与点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（　　）

• A． 4
• B． 5
• C． 6
• D． 7

Answer 1

分析 如图，作N关于AD的对称点N′，连接MN′，作BN″⊥AC于N″交AD于M′．因为BM+MN=BM+MN′≤BN″，所以当M与M′，N与N″重合时，BN″最小，求出BN″即可解决问题．

解答 解：如图，作N关于AD的对称点N′，连接MN′，作BN″⊥AC于N″交AD于M′．

∵BM+MN=BM+MN′≤BN″，
∴当M与M′，N与N″重合时，BN″最小，
∵$\frac{1}{2}$×AC×BN″=15，AC=6，
∴BN″=5，
∴BM+MN的最小值为5，
故选B．

点评 本题考查轴对称-最短问题、垂线段最短等知识，解题的关键是重合利用对称，垂线段最短解决最值问题，属于中考常考题型．